2 zadania Rodney: Trapi mnie pewne zadanie A nawet dwa 1) Niech liczby rzeczywiste x,y spelniaja rownosc (x+5)²+(y−12)²=14² Wtedy wyrazenie x²+y² ma najmniejszą wartość równą: ? 2)Ile podzbiorów ma zbiór {a,{a},{{a}}} ? Szczególnie drugie prosiłbym z jakimś bardziej rozbudowanym wyjaśnieniem. W pierwszym w sumie tez chcialbym sie dowiedzeic skad wzial sie wynik Z gory dziekuje

Basia: każdy zbiór n−elementowy ma 2ⁿ (n≥1) podzbiorów (razem z pustym i samym sąbą) czyli 2³ = 8 dowód jest indukcyjny: 1. n=1 czyli mamy zbiór A={a} jego podzbiory to: ∅; {a} czyli 2=2¹ 2. A= {x₁,....,x_n} zakładamy, że ma 2ⁿ podzbiorów B = {x₁,....,x_n,x_n+1} każdy z podzbiorów A jest podzbiorem B czyli mamy 2ⁿ do każdego z tych istniejącym możemy dołożyć x_n+1 tworząc 2ⁿ nowych co daje razem 2ⁿ + 2ⁿ = 2*2ⁿ = 2ⁿ⁺¹ c.b.d.u.

Rodney: przyznam, ze nie wiem co dalej...

Basia: co dalej ? nic dalej! nie łapię o co Ci chodzi

Rodney: wydaje mi sie, ze to nie jest odpowiedz na zadne z tych pytan

Mila: Liczba wszystkich podzbiorów zbioru n− elementowego A={a₁,....a_n}

n 0
	=1 zbiór pusty

n 1
	liczba podzbiorów 1− elementowych

n 2
	liczba podzbiorów − elementowych

. .

n n
	=1 zbiór A

suma :

n 0		n 1		n 2		n 3		n n
	+		+		+		+........+		=(1+1)n =2n

współczynniki dwumianu Newtona dla dwumianu (1+1)

Basia: pytasz ile podzbiorów ma zbiór trzyelementowy (bo Twój zbiór jest trzyelementowy) ma ich 2³ = 8 a wynika to z przytoczonego i udowodnionego twierdzenia

Rodney: no ok, zastanawialy mnie po prostu te nawiasy wewnatrz zbioru... A co z zadaniem 1. ?

ZKS: To ja sobie zrobiłem 1 zadanie. f(x , y) = x² + y² φ(x , y) = (x + 5)² + (y − 12)² − 14² F(x , y , λ) = x² + y² + λ((x + 5)² + (y − 12)² − 14²)) x² + y² + λ((x + 5)² + (y − 12)² − 14²)) = = x² + y² + λx² + 10λx + 25λ + λy² − 24λy + 144 − 196λ

	dF
{		= 2x + 2λx + 10λ
	dx

	dF
{		= 2y + 2λy − 24λ
	dy

{φ(x , y) = (x + 5)² + (y − 12)² − 14²

	5λ
{(1 + λ)x = −5λ ⇒ x = −
	1 + λ

	12λ
{(1 + λ)y = 12λ ⇒ y =
	1 + λ

{x² + 10x + 25 + y² − 24y + 144 − 196 = 0

	5λ		5λ		12λ		12λ
(−		)2 + 10 * (−		) + (		)2 − 24 * (		) − 27 = 0
	1 + λ		1 + λ		1 + λ		1 + λ

169λ2		388λ
	−		− 27 = 0 / * (1 + λ)2
(1 + λ)2		1 + λ

−196λ² − 392λ − 27 = 0

	1		27		1		27
−196(λ +		)(λ +		) = 0 ⇒ λ = −		∨ λ = −
	14		14		14		14

	1
Dla λ = −
	14

	5		12
x =		∧ y = −
	13		13

	27
dla λ = −
	14

	135		324
x = −		∧ y =
	13		13

Basia: skoro (x+5)²+(y−12)²=14² (y−12)² = 14² − (x+5)² y − 12 = ±√14² − (x+5)² y = ±√14² − (x+5)² + 12 x² + y² = x² + (√14² − (x+5)²+12)² lub x² + y² = x² + (−√14² − (x+5)²+12)² czyli wypadałoby znaleźć najmniejszą wartość każdej z funkcji f(x) = x² + (√14² − (x+5)²+12)² g(x) = x² + (−√14² − (x+5)²+12)² ale to paskudne liczenie, więc powinien być jakiś prostszy sposób

ZKS: Rodney a jakie masz odpowiedzi do 1 zadania?

Rodney: odpowiedzi to 2 1 √3 √2

ZKS: Skąd tyle odpowiedzi jeszcze √3 i √2 niech ktoś mądrzejszy jak tak zrobi to zadanie. Mi w 1 zadaniu wyszło 1 i 729.

Basia: to niemożliwe ! jak mogą być cztery różne wartości najmniejsze ? przytocz te odpowiedzi dokładnie !

Basia: może to są współrzędne; np. dla x=2 y=1 i dla x=√3 y=√2 albo coś w tym rodzaju

ZKS: Właśnie ciekawe o co chodzi ale jeżeli to są współrzędne to nie spełniają warunku okręgu.

Basia: wydaje mi się, że to zadanie może mieć nieco inną treść (ale oczywiście pewna nie jestem)

ZKS: Chyba że może to są odpowiedzi do wyboru A 2 B 1 C √3 D √2?

Basia: a to możliwe, ale wtedy to byłby banał

ZKS: Nie ma osoby piszącej tutaj to zadanie więc nie będziemy się głowić co miał na myśli. Ja już idę na spanie więc dobranoc Basia .

Basia: Dobranoc

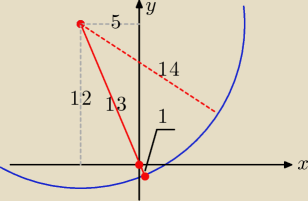
Teo: Zadanie 1) odp.: 1 Zadanie 2) ile podzbiorów ma zbiór {a} ? ile podzbiorów ma zbiór {{a}} ?