Geometria analityczna adasb17: Punkty K=(−8,−5), L=(4,0), M=(4,5) są kolejnymi wierzchołkami równoległoboku KLMN. Wiedząc że punkt S=(−2,0) jest punktem przecięcia się przekątnych, wyznacz: a) współrzędne wierzchołka N, b) równania przekątnych równoległoboku, c) pole równoległoboku.

adasb17: help.

adasb17: Pomocy

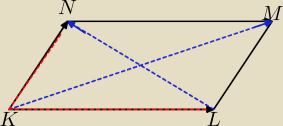
Gustlik: K=(−8,−5), L=(4,0), M=(4,5), N=(x, y) Wektorami: ad a) KL^→=[4−(−8), 0−(−5)]=[12, 5] NM^→=KL^→=[12, 5] NM^→=[4−x, 5−y] 4−x=12 −x=8 x=−8 5−y=5 y=0 N=(−8, 0) ad b) też z wektorów K=(−8,−5), L=(4,0), M=(4,5), N=(−8, 0) KM^→=[4−(−8), 5−(−5)]=[12, 10]

	10		5
a=		=
	12		6

	5
y=		x+b
	6

Podstawiam wspołrzędne któregoś z pktów, np. M

	5
5=		*4+b /*6
	6

30=20+6b 10=6b /:6

	10		5
b=		=
	6		3

	5		5
y=		x+
	6		3

LN^→=[−8−4, 0−0]=[−12, 0]

	0
a=		=0
	−12

funkcja stała y=0 ad c) też z wektorów K=(−8,−5), L=(4,0), M=(4,5), N=(−8, 0) KL^→=[4−(−8), 0−(−5)]=[12, 5] KN^→=[−8−(−8), 0−(−5)]=[0, 5] Wyznacznik wektorów d(KL^→, KN^→)= | 12 5 | | 0 5 | =12*5−5*0=60 Pole=|d(KL^→, KN^→)|=60