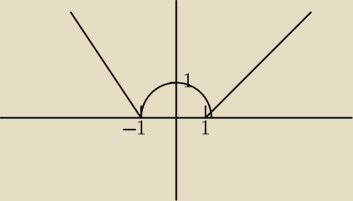
pochodne Dominika: Narysowac wykres funkcji i wskazac punkty w ktorych funkcja nie ma pochodnych, udowodnic to za pomoca granic jednostronnych. f(x) = |x²−1| wiec wykres wyglądać będzie tak. I teraz pytanie: czemu granica po x→−1⁻ = −2 a po x→−1⁺ = 2 11

Artur_z_miasta_Neptuna: źły wzór funkcji f(x)=

⎧	|x−1| dla x∊R\<−1,1>
⎩	−x2+1 x∊<−1,1>

Artur_z_miasta_Neptuna: też źle napisałem: f(x) =

⎧	−x−1 dla x∊(−∞,−1)
⎨	−x2+1 dla x∊<−1,1>
⎩	x−1 dla x∊(1,+∞)

Artur_z_miasta_Neptuna: chyba że tam po lewej i prawej to są ramiona paraboli a to przypadkiem nie chodziło o wyliczenie pochodnej w punkcie z granicami lewo i prawostronnymi? Bo przecież granica lewo i prawostronna FUNKCJI (a nie pochodnej) w −1 i 1 będzie wynosić '0' ... w końcu jest to funkcja ciągła

Basia: Artur 1. to jest funkcja f(x) = |x²−1| Dominika nie umiała narysować łuków 2. oczywiście, że chodzi o granice ilorazów różnicowych, skoro należy udowodnić, że w punktach −1 i 1 funkcja nie jest różniczkowalna

Pain:

	f(x)−f(x0)
To chyba trzeba wyliczyc ze wzoru f'(x0)=limx→x0		ale pewny nie
	x−x0

jestem może niech ktoś inny sie wypowie...

pigor: {P{Pain]] masz całkowitą rację w "ostrzach" , czyli tu w x=±1 nie będzie pochodnych i aby to wykazać trzeba się "pobawić" w tych granicach (tu definicja pochodnej w x_o=−1^± i x_o=1^±) , czy istnieją

kapek: Jaka jest w końcu postać tej funkcji? Bo z rysunku pewności nie mamy, ale wystarczy policzyć te granice w 1+ i 1− oraz −1+ a także −1− i jeśli są one różne to pochodna nie istnieje w tym punkcie. Jeszcze były inne warunki, które sprawiają, że nie istnieje pochodna z IxI

kapek: Pochodna z | x²−1 | dla przedziału (−1,1) wynosi −2*x, natomiast w pozostałych przedziałach dziedziny wynosi 2x. Ponieważ w punktach −1 oraz 1 pochodna nie jest ciągła, czyli nie istnieje. Można w tym celu wykorzystać podróżniczkę(subróżniczkę). Pochodną wartości bezwzględnej jest sgn(x), które nie jest określone dla "0". Naszym x jest tutaj x²−1, a "0" wartości −1 oraz 1