Oblicz pole obszaru ograniczonego przez krzywe
alku: Oblicz pole obszaru ograniczonego przez krzywe:
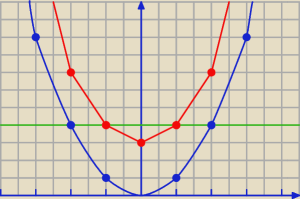
y=x2
y=x2+3
y=4
12 cze 01:31
Godzio:
P = 2 * [ ∫
01(x
2 + 3 − x
2)dx + ∫
12(4 − x
2)dx ] =
| | x3 | | 8 | | 1 | |
= 2 * [ 3x|01 + (4x − |
| )|12 ] = 2 * [ 3 + 8 − |
| − 4 + |
| ] = |
| | 3 | | 3 | | 3 | |
| | 7 | | 14 | | 28 | |
= 2 * [ 7 − |
| ] = 2 * |
| = |
| |
| | 3 | | 3 | | 3 | |
12 cze 03:48
Mila: Godzio−
12 cze 14:59
alku: Dzieki, rozumiem tok myslenia ale w odpowiedziach jest 14/3
(Gewert Skoczylas, Kolokwia i
Egzaminy, Egzamin Poprawkowy 1, GR B, zadanie 3)
Zreszta i faktycznie 28/3 jest za duzym wynikiem bo jak tam zmiescic prawie 10prostokatow
12 cze 16:36
alku: aha sorry skala wymieszana
12 cze 16:39
Basia:
na prostokąty nie ma co patrzeć, bo na różnych osiach są różne jednostki
na osi OX 1=2 kratki na osi OY 1=1 kratka
wynik jest dobry, a w Skoczylasie podano wynik dla połowy tego obszaru, bo to własnie liczymy i
potem tylko mnożymy przez 2
12 cze 16:43