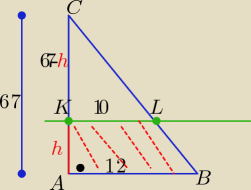
Geometria Milord: W trójkącie prostokątnym o przyprostokątnych AC = 67cm i AB = 12cm poprowadzono prostą równoległą do boku AB, która przecina bok AC w punkcie k i bok BC w punkcie l. Odcinek kl ma długość 10cm. Oblicz pole powstałego trapezu ABLK.

Eta: 1 sposób

	12		67
Z tw. Talesa		=
	10		67−h

wyznacz h =....

	12+10
P(trABKL) =		*h =....
	2

2 sposób P(tr, ABKL)=P(ΔABC) − P(ΔKLC)=.....

Milord: coś mi nie pykło zbytnio , wychodzi mi 181,17

Milord: to jak ma byc ?

Eta:

	67
h=
	6

	67
P= 11*		=...
	6