Rozwiązania równania, parametr m
Kuba: Jak rozwiązać następujące zadanie:
zbadaj liczbę rozwiązań równania w zależności od parametru m.
Z góry dziękuję

Basia:
x≠1
1.
wartość bezwzględna ≥ 0 ⇒ dla m<0 nie ma rozwiązania
2.
m = 0
3x−1 = 0
x =
13
dla m=0 jedno rozwiązanie
3.
m>0
lub
3x−1 = m(x−1)
lub
3x−1 = −m(x−1)
3x − 1 = mx − m
lub
3x − 1 = −mx + m
3x − mx = 1−m
lub
3x+mx = 1+m
(3−m)x = 1−m
lub
(3+m) = 1+m
dla m = 3
pierwsze 0 = −2 sprzeczność, ale drugie 6x=4 ma jedno rozwiązanie
dla m= −3
drugie 0 = −2 sprzecznośc, ale pierwsze 6x= 4 ma jedno rozwiązanie
dla m≠ ±3
mamy dwa rozwiązania
ale trzeba jeszcze wykluczyć x=1 czyli
1−m ≠ 3−m
−2 ≠ 0 czyli w porządku, nic nie wykluczamy
1+m ≠ 3+m
−2 ≠ 0 czyli w porządku, nic nie wykluczamy
zbierz to teraz do kupy i ładnie zapisz rozwiązanie
Eta:
 2sposób
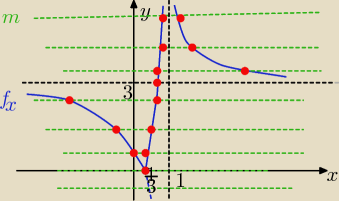
2sposób (graficznie)
| 3x−1 | | 3(x−1)+2 | | 2 | |
| = |
| = 3+ |
| , x≠1 |
| x−1 | | x−1 | | x−1 | |
| | 2 | | 2 | |
f(x) = I3+ |
| | −−− rysujemy wykres : 3+ |
| i tę część spod osiOX odbijamy nad |
| | x−1 | | x | |
oś OX
0 rozwiązań dla m < 0
1 rozwiązanie dla m=0 lub m= 3
2 rozwiązania dla m€ (0,3) U (3,
∞)

 2sposób (graficznie)
2sposób (graficznie)