Punkty A(-2,-4), B(5,-3), C(6,0) i D(1,5) są wierzchołkami czworokąta ABCD Dominika: Punkty A(−2,−4), B(5,−3), C(6,0) i D(1,5) są wierzchołkami czworokąta ABCD a) Wykaż, że przekątne AC i BD są do siebie prostopadłe b) Oblicz pole czworokąta ABCD

Basia: ad.a jeżeli przerabialiście wektory to policz iloczyn skalarny AC^→ →i BD^→ a jeżeli nie to napisz równania pr.AC i pr.BD i skorzystaj z warunku prostopadłości prostych (równania w postaci kierunkowej) a₁*a₂ = −1 ad.b napisz najpierw czy znasz wektory, bo nie chce mi się pisać bez potrzeby

Dominika: Potrzebuję tylko podpunktu b

Dominika: Nie znam

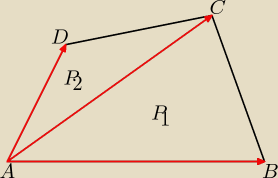
Gustlik: Punkty A(−2,−4), B(5,−3), C(6,0) i D(1,5) są wierzchołkami czworokąta ABCD a) Wykaż, że przekątne AC i BD są do siebie prostopadłe b) Oblicz pole czworokąta ABCD WEKTORY, WEKTORY, WEKTORY ! ad a) I sp. AC^→=[6−(−2), 0−(−4)]=[8, 4]

	4		1
aAC=		=
	8		2

BD^→=[1−5, 5−(−3)]=[−4, 8]

	8
aBD=		=−2
	−4

spełniony jest warunek prostopadłości prostych. II sp. z iloczynu skalarnego wektorów, iloczyn skalarny=0 dla wektorów prostopadłych AC^→*BD^→=8*(−4)+4*8=−32+32=0 cnd. b) z wyznacznika wektorów A(−2,−4), B(5,−3), C(6,0) i D(1,5) AB^→=[5−(−2), −3−(−4)]=[7, 1] AC^→=[6−(−2), 0−(−4)]=[8, 4] AC^→=[1−(−2), 5−(−4)]=[3, 9] Liczę pole trójkąta ABC P₁ wyznacznik wektorów d(AB^→, AC^→)= | 7 1 | | 8 4 | =7*4−1*8=28−8=20

	1		1
P1=		|d(AB→, AC→)|=		*|20|=10
	2		2

Liczę pole trójkąta ACD P₁ wyznacznik wektorów d(AC^→, AD^→)= | 8 4 | | 3 9 | =8*9−4*3=72−12=60

	1		1
P2=		|d(AC→, AD→)|=		*|60|=30
	2		2

P=P₁+P₂=10+30=40

Dominika: Nie da się tego zrobić innym sposobem? Bo wyznacznika wektorów nie robiliśmy

Gustlik: Dominika wektory są proste jak konstrukcja młotka, wzór na ich współrzędne jest tutaj: https://matematykaszkolna.pl/strona/1623.html , a na iloczyn skalarny tutaj: https://matematykaszkolna.pl/strona/1629.html i https://matematykaszkolna.pl/strona/1630.html . Natomiast wyznaczniki wektorów i obliczanie pól za ich pomocą opisałem tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 . Lepiej się naucz wektorów, bo to PODSTAWA GEOMETRII ANALITYCZNEJ. Z takie zadaniem jak to bez wektorów jest kupa roboty, dużo żmudnych obliczeń i łatwo o pomyłke, zajmie ci ono pół dnia i ze dwie kartki A4. Mniej czasu zajmie Ci nauczenie się wektorów choćby z tej strony, niż rozwiązanie tego zadania bez nich. Poza tym będzie Ci łatwiej z innymi zadaniami, bo wektory przydają się niemal we wszystkich zadaniach z geometrii analitycznej.

Dominika: Rozumiem, ale chodzi o to, że w ogóle nie przerabialiśmy czegoś takiego na lekcji i dziwne to będzie jak oddam kartkę z zadaniem zrobionym takim sposobem

Dominika: Współrzędne były, ale iloczynu skalarnego, kąta między wektorami ani wyznaczników wektorów nie było

Gustlik: Nauczycielka MUSI uznać tak rozwiązane zadanie, matematyczka POWINNA znać ten sposób. Jeżeli nie uzna − to trzeba interweniować u niej, potem u wychowawczyni, u dyrektora, a jak to nie pomoże − do kuratorium. Poza tym Ty się uczysz nie dla nauczycielki, tylko dla siebie, w dodatku CKE na maturze honoruje każdą poprawna metodę, nawet taką, której nie ma na lekcjach. Masz po prostu zadanie zrobić dobrze. Wektorami zadania rozwiązuje się krócej i prosciej, znając ten sposób zaoszczędzisz sporo cennego czasu i na maturze i na sprawdzianie, a ten zaoszczędzony czas wykorzystasz na inne zadania i wynik będzie lepszy.

Gustlik: Co z tego, że nie było? Masz prawo znać te zagadnienia i je stosować w zadaniach, zwłaszcza, że są banalnie proste. Jeszcze raz powtarzam − nauczycielka MUSI uznać tak rozwiązane zadanie.

Gustlik: Zadanie https://matematykaszkolna.pl/forum/149765.html zrób tym samym sposobem.

Dominika: Dzięki Spróbuję zrobić. Ale mógłbyś mi podać sam wynik, żeby wiedzieć czy dobrze zrobiłam. Nie chcę rozwiązania tylko wynik

pigor: ... lub jeśli nie masz wskazanego sposobu (narzędzi) do obliczenia tego pola, to narysuj sobie dany czworokąt na kratkowanym papierze i ... licząc odpowiednio np. tak: : P_ABCD= 8*9−1²−¹₂(1*3+1*7+5*5+3*9)= = 72−1−¹₂(3+7+25+27)= 71−¹₂*62= 71−31= 40 j² . ...

Dominika: Gustlik czy ma wyjść w tym zadaniu https://matematykaszkolna.pl/forum/149765.html 32?

Basia: dla tych, którzy nie znają wektorów: wystarczy policzyć |AC| i napisać równanie pr.AC

	|AC|*d(B; pr.AC)
PABC =
	2

	|AC|*d(D; pr.AC)
PADC =
	2

Gustlik: Basiu, tym, co nie znają wektorów polecam zapoznanie sie z nimi, bo zaproponowana przez Ciebie metoda obliczania pola trójkąta to najdłuższa i najtrudniejsza metoda z możliwych. To właśnie ta metoda powinna być na rozszerzeniu, a wektorowa na podstawach. Pozdrawiam

Gustlik: Punkty A(−1,−2) B (5,2) C(0,4) i D(−3,2) są wierzchołkami trapezu ABCD. Oblicz pole tego trapezu AB^→=[5−(−1), 2−(−2)]=[6, 4] AC^→=[0−(−1), 4−(−2)]=[1, 6] AD^→=[−3−(−1), 2−(−2)]=[−2, 4] d(AB^→, AC^→)= | 6 4 | | 1 6 | =6*6−4*1=36−4=32

	1
P1=		|d(AB→, AC→)|=16
	2

d(AC^→, AD^→)= | 1 6 | | −2 4 | =1*4−6*(−2)=4+12=16

	1
P2=		|d(AC→, AD→)|=8
	2

P=P₁+P₂=16+8=24 Gdzieś masz błąd, skoro wyszło Ci 32. Pozdrawiam