geometria analityczna Soldier: Witam zadanko z geometrii punkt A=(−7,2) należy do okręgu stycznego do osi x w punkcie (−3,0) napisz równanie tego okręgu

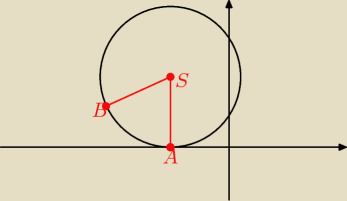
Basia: A(−3,0) ⇒ S(−3,b) B(−7,2) no i trzeba zbadać dla jakiego b |SA| = |SB|

niebieski: środek okręgu leży zawsze nad punktem styczności, więc jego wspołrzędna x=−3 a wspołrzędna y jest taka sama jak promień ⇒ (x−p)²+(y−q)²=r²korzystam z punktu A ⇒ (−7+3)²+(2−r)²=r² 16+(2−r)²=r² 16+4−4r+r²=r² r=5 (x+3)²+(y−5)²=25

Soldier: ok to szukam promienia

gość: Masz do rozwiązania układ równań, bo oba punkty należą do okręgu: (−3−x_s)²+(0−y_s)²=r² (−7−x_s)²+(2−y_s)²=r² oraz dodatkowa informacja, że: x_s=−3 i y_s>0, bo styczny w p. (−3,0) i A należy do okręgu, a jego wsp. y_a>0

Soldier: dziękuję wam bardzo

pigor: ... otóż, S=(−3,y)=? − szukany środek okręgu i r=y=? − szukana długość jego promienia (y>0), to z warunków zadania : |AS|=y ⇔ AS²=y² ⇔ (−3+7)²+(y−2)²=y² ⇔ 16+y²−4y+4=y² ⇔ 4y=20 ⇔ ⇔ y=5 , zatem (x+3)²+(y−5)²=25 − szukane równanie okręgu . ...