Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Kamil: W ostrosłupie prawidłowym czworokątnym przekątna podstawy jest równa 8√2 a krawędź ściany bocznej 12 cm. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

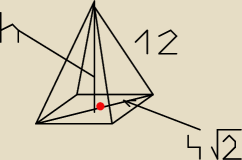
jasiu: tam gdzie czerwona kropka kąt prosty. Powstaj tam wtedy trojkąt prostokątny. i z Tw. Pitagorasa można policzyć wysokość 12² − (4√2)² = h² h = √112 =

jasiu: h = 2√28

jasiu: i teraz w podstawie mamy przekątną równą 8√2 przyrownujemy to do wzoru ze a√2 = 8√2 a = 8 Pp = 8² = 64

jasiu: V = ¹₃ * Pp * h V = ¹₃ * 64 * 2√28 = ^128√28₃ cm ³

jasiu: i teraz mamy h i polowe boku czyli 4 to z Tw Pitagorasa mzoemy wysokosc siany bocznej