Ile liczb 5-cyfrowych ma sumę cyfr równą 22? Szybcior: Ile liczb 5−cyfrowych ma sumę cyfr równą 22?

Szybcior: Jak ktoś by miał chęć to może spróbować rozwiązać to zadanie Oblicz pole figury ograniczonej osiami układu współrzędnego i wykresami funkcji: x−3−y=0 x−y=19

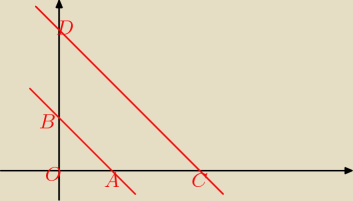
Basia: to są proste y = x−3 y = x−19 czyli równoległe P = P_tr.COD − P_tr.AOB =

OC*OD		OA*OB
	−
2		2

zastanów się jakie są długości tych odcinków; podstaw i gotowe

Eryk: nie daje rady

Basia: 22 = 9+9+4+0+0 22 = 9+9+3+1+0 22 = 9+9+2+2+0 22 = 9+9+2+1+1 22 = 9+8+5+0+0 22 = 9+8+4+1+0 22 = 9+8+3+2+0 22 = 9+8+3+2+1 22 = 9+7+6+0+0 22 = 9+7+5+1+0 22 = 9+7+4+2+0 22 = 9+7+4+1+1 22 = 9+7+3+3+0 22 = 9+7+3+2+1 22 = 9+7+2+2+2 22 = 9+6+6+1+0 22 = 9+6+5+2+0 22 = 9+6+5+1+1 22 = 9+6+4+3+0 22 = 9+6+4+2+1 22 = 9+5+5+3+0 22 = 9+5+5+2+1 22 = 9+5+4+4+0 22 = 9+5+4+3+1 22 = 9+4+4+3+2 i teraz jeszcze należałoby policzyć ile liczb z każdego zestawu można zbudować przydałaby się prostsza metoda, ale o tak wczesnej porze mój mózg jeszcze za bardzo nie działa

Basia: w jakich punktach proste y = x−3 i y=x−19 przecinają osie układu współrzędnych ? na osi OX y=0 czyli podstawiasz za y 0 i wyliczasz x dostaniesz współrzędne A i C na osi OY x=0 czyli podstawiasz za x 0 i wyliczasz y dostaniesz współrzędne B i D

Basia: ad. wpis z 10:27 to jeszcze nie wszystko 22 = 8+8+6+0+0 itd. musi być prostszy sposób

pigor: ... ja widzę to tak : doprowadzę dane równania do postaci odcinkowej prostej : x−3−y=0 i x−y=19 ⇔ x−y=3 i x−y=19 ⇔ ^x₃+^y₋₃=1 i ^x₁₉+^y₋₁₉=1 ⇒ ⇒ P= ¹₂*19²−¹₂*3² = ¹₂(19²−3²)= ¹₂(19−3)(19+3}= = ¹₂*16*22= 4*22= 88 j² − szukane pole między danymi prostymi . ...

Basia: Dzień dobry. Chyba za wcześnie jeszcze jest ¹₂*16 =8

pigor: ... dzięki masz rację idę w plener . ...

John Brawo : a co z 1 zadaniem ?

PW: Dokończyć wyliczankę zaczętą przez Basię (bo to jeszcze nie wszystkie możliwe rozkładu 22 na 5−składnikowe sumy) i przestawiać różniące się składniki tak, by zero nie było na pierwszym miejscu).

PW: Wydaje się to jednak żmudne. Mam koncepcję (to na razie luźny pomysł) pożenić ze sobą sumy 3−składnikowe i 2−skladnikowe. Te pierwsze muszą mieć co najmniej sumę 4 (bo dwa składniki dokładane do trzech nie przekraczają 18). Sumy dwuskładnikowe mogą być dowolne od 0 do 18. Mielibyśmy wtedy następujące sumy (na pierwszym miejscu powstałe z sumowania 3 składników, na drugim powstałe z sumowania 2 składników): 4+18, 5+17, 6+16, 7+15, 8+14, 9+13, 10+12, 11+11, 12+10, ,13+9 14+8, 15+7, ,16+6 17+5, 18+4, 19+3, 20+2, 21+1, 20+0 Gdyby udało się bez wypisywania policzyć na ile sposobów można utworzyć poszczególne sumy 3− i 2− składnikowe, to może byłoby szybciej.

PW: A tak w ogóle to mógłbyś napisać: jest to łatwe zadanie z informatyki, czy matematyka dyskretna ze studiów?

Mila: PW to jest zadanie dla komputera, albo zadanie dla sierotki Marysi zadane przez złą macochę ( zmiast wybierania maku z piasku)..

PW: Jeżeli sierotka zauważy, że dla liczby n o sumie cyfr 22 liczba (n−1) jest podzielna przez 3 (bo ma sumę cyfr 21, 30 lub 39 w zależności od liczby zer na końcu), to będzie badać co trzecią liczbę − i może zdąży na bal. Komputer też się mniej zasapie. Szybcior pewnie znalazł rozwiązanie w innym miejscu, bo już tu nie zagląda, więc ja też dam sobie spokój.