Oblicz pole tego trójkąta oraz dł. wszystkich jego wysokości. Kasia: Boki trójkąta mają długość 13, 13 i 10. Oblicz pole tego trójkąta oraz dł. wszystkich jego wysokości.

Matematyk.....: Trójkąt jest równoramienny. czyli, h−wysokość przy podstawie h²+5²=13² h²=169−25 h²=144 h=√144 h=12 H− wysokość kolejnych boków. Skoro trójkąt jest równoramienny to 2 pozostałe boki będą miały wysokość taka sama. H²+6,5²=13² H²=169−42.25 H²=126.75 H=√126.75 Pole 1/2 a•h 1/2 10•12=60 [cm²]

Kasia: dzięki wielkie : )

Marek: Witam. Pierwsza h=12, ale 2 i 3 nie może być już wyliczona z tw. Pitagorasa ponieważ te dwie wysokości nie opadają idealnie na połowę boku i powinniśmy je wyliczyć z pola P=1/2*10*12 P=60 P=(a*h)/2/*2 2p = a*h/:a H=2p/a H=(2*60)/13 = 120/13 ≈ 9,23 Druga i trzecia wysokość mają po 9,23

Filip: inaczej, polecam to zaokrąglić do dwóch cyfr znaczących 9.23 ≈ 9.2

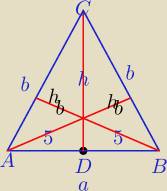
Iryt: Dane: a=10, b=13 Szukane: P_Δ, wysokości Δ 1) h²=13²−5²=144 h=12

	10*12
PΔ=		=60
	2

2)

	13*hb
60=
	2

	120
hb=
	13

h_b=9³₁₃ I koniec.