pytanie tn: czy zachodzi? x⇒ y ⇔ y ⇒x

Trivial: Sam możesz sprawdzić (tabelką)!

tn: 0 ⇒ 1 1 1 ⇒ 0 0 1 ⇒ 1 1 0 ⇒ 0 1 Więc powinno teraz zachodzić: 1 ⇒ 0 0! 0 ⇒ 1 1 0 ⇒ 0 1 1 ⇒ 1 1 mam niestety zero przy wykrzykniku czyli nie zachodzi prawda?

Trivial: Nie zachodzi. http://www.wolframalpha.com/input/?i=%28x+implies+y%29+equivalent+%28y+implies+x%29

tn: a czy prawidłowo rozpisałem?

Trivial: Powinien być jeszcze wykrzyknik przy 0 ⇒ 1 w drugiej tabelce (0 nie jest ⇔ 1)

tn: Ok, a więc mam zadanie Udowodnij, że jeśli zachodzi równość z sinusami(nie będę jej tu przepisywał) to trójkąt jest prostokątny. Więc nie mogę udowodnić odwrotnie, tzn założę, że trójkąt jest prostokątny i pokażę, że zachodzi taka równość?

Trivial: Nie możesz.

tn: właśnie ze względu na to prawo?

tn: co pokazałem, że nie zawsze zachodzi?

Trivial: To po prostu nie działa.

tn: ale przecież był jakiś typ dowodu − wyjście od założenia i dojście do tezy

Trivial: Wyjście od założenia i dojście do tezy to 'normalny' dowód. Jest dowód nie wprost. Wychodzisz z tezy i pokazujesz, że prowadzi to do sprzeczności z założeniem.

tn: nie rozumiem czegoś tutaj. Setki razy miałem okazję przeczytać w literaturze. Założmy że tak jest, to oznaczałby skolei,ale jest to niemożliwe ..... .........

Trivial: To dowód nie wprost.

tn: więc powinienem zaprzeczyć tezie, i pokazać że jest to absurd w stosunku do założenia czyli. Założę, że trójkat jest nieprostokątny. Powinna wyjść sprzeczność z założeniem tej równości tryg?

Trivial: Jeżeli wykażesz że równość ta nie zachodzi dla trójkąta innego niż prostokątny to wciąż będziesz musiał udowodnić, że dla trójkąta prostokątnego jednak zachodzi.

tn: więc jak zrobić tu nie wprost?

Trivial: Tak jak powiedziałeś. Ale trzeba będzie jeszcze oddzielnie udowodnić, że dla trójkąta prostokątnego równość zachodzi (wtedy możesz już wyjść z tezy i dojść do założenia stosując przekształcenia jednoznaczne).

Trivial: Może jednak przepisz tę równość... Są szanse, że istnieje prostsza wersja dowodu.

tn: wzory redukcyjne zachodzą zawsze? czy tylko w trójkącie prostokątnym

tn: czyli czy nawet dla alfy równej 105 ?

Trivial: Zachodzą zawsze. 105 = 90 + 45 − 30

tn: a jedynka trygonometryczna?

Trivial: też.

tn: Jeżeli w trójkącie zachodzi sin² (α) = sin²(β) + sin²(α+β) to trójkąt jest prostokątny α+β+γ=180 γ=180 (α+β) Moje spostrzeżenie jest takie: δ = α+β sin²(α+β) = sin²(δ) = sin²(180−δ)= sin²(180−(α+β)) = sin²(γ) nie wiem co dalej?

tn: trza to udowodnić

Maslanek: Z twierdzenia sinusów udowodnij.

tn: pokaż mi to

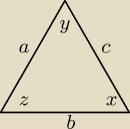
Maslanek: Przyjmuję takie oznaczenia, bo nie chce mi się klikać na alfy zbyt często.. Z twierdzenia sinusów:

a		c		b		c		a		b
	=		oraz		=		, oraz		=		.
sin x		sin z		sin y		sin z		sin x		sin y

Po przekształceniach:

	c sin x		b sin z		a sin y
a=		oraz c=		, oraz b=		.
	sin z		sin y		sin x

Jeśli trójkąt będzie prostokątny, to: a²+b²=c². Udowodnij ^^.