.
Paula: W okręgu o śr AB rysujemy cięciwe CD równaległa do AB. Udowodnij ze róznica miar kątów ACD do
CDA jest równa 90 stopni.
9 cze 20:20
Eta:
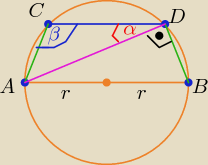
|∡ACD|=
β , |∡CDA|=
α , |∡ADB|= 90
o −−− jako kąt wpisany oparty na średnicy
Czworokąt ABCD jest rapezem równoramiennym ⇒ |∡ACD|= |∡CDB|
zatem β= α+90
o ⇒ β−α= |∡ADC|− |∡CDA|= 90
o
c.n.u
9 cze 20:52
Aga1.:
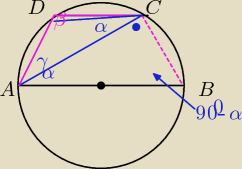
Mam udowodnić, że β−α=90
0.
Kąt BAC=kątowi ACD=α, są to kąty naprzemianległe
Kąt ACB=90
0−−kąt wpisany oparty na średnicy.
β+90
0−α=180
0 własność kątów wpisanych.
β−α=90
0
9 cze 20:53
 |∡ACD|=β , |∡CDA|= α , |∡ADB|= 90o −−− jako kąt wpisany oparty na średnicy
Czworokąt ABCD jest rapezem równoramiennym ⇒ |∡ACD|= |∡CDB|
zatem β= α+90o ⇒ β−α= |∡ADC|− |∡CDA|= 90o
c.n.u
|∡ACD|=β , |∡CDA|= α , |∡ADB|= 90o −−− jako kąt wpisany oparty na średnicy
Czworokąt ABCD jest rapezem równoramiennym ⇒ |∡ACD|= |∡CDB|
zatem β= α+90o ⇒ β−α= |∡ADC|− |∡CDA|= 90o
c.n.u
 Mam udowodnić, że β−α=900.
Kąt BAC=kątowi ACD=α, są to kąty naprzemianległe
Kąt ACB=900−−kąt wpisany oparty na średnicy.
β+900−α=1800 własność kątów wpisanych.
β−α=900
Mam udowodnić, że β−α=900.
Kąt BAC=kątowi ACD=α, są to kąty naprzemianległe
Kąt ACB=900−−kąt wpisany oparty na średnicy.
β+900−α=1800 własność kątów wpisanych.
β−α=900