Geometria analityczna adasb17: Punkty A= (1, 2) , B=(7, 3), C= (2, 8) są wierzchołkami trójkąta ABC. Napisz równania prostych zawierających wysokości trójkąta ABC. Proszę o wytłumaczenie

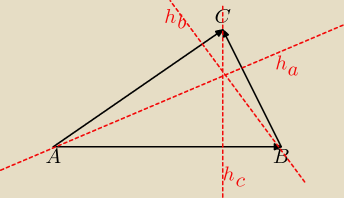
Gustlik: A= (1, 2) , B=(7, 3), C= (2, 8) Liczę prostą h_c Z wektorów liczę współczynnik kierunkowy: AB^→=[7−1, 3−2]=[6, 1]

	1
aAB=
	6

Pr. h_c ⊥ AB

	1
a=−		=−6
	aAB

y=−6x+b Podstawiam współrzedne pktu C leżącego na tej prostej: 8=−6*2+b 8=−12+b b=20 Pr. h_c: y=−6x+20 Liczę prostą h_b A= (1, 2) , B=(7, 3), C= (2, 8) AC^→=[2−1, 8−2]=[1, 6]

	6
aAC=		=6
	1

Pr. h_b ⊥ AC

	1
a=−
	6

	1
y=−		x+b
	6

Podstawiam wsp. B

	1
3=−		*7+b /*6
	6

18=−7+6b 18+7=6b 6b=25 /:6

	25
b=
	6

	1		25
Pr. hb: y=−		x+
	6		6

Liczę prostą h_a A= (1, 2) , B=(7, 3), C= (2, 8) BC^→=[2−7, 8−3]=[−5, 5]

	5
aBC=		=−1
	−5

Pr. h_a: a=1 y=x+b Wstawiam wsp. A: 2=1+b b=1 Pr. h_a: y=x+1

Mila: wektor AB=[6,1] h_c prostopadła do AB 6x+1y+C=0 równanie ogólne prostej (Ax+By+C=0) obliczam C 6*2+1*8+C=0 C=−20 h_c: 6x+y−20=0 Podobnie pozostałe wysokości

pigor: ... coś mi nie gra powyżej , bo AB^→=[6,1] ⇒ AB^→⊥CD^→=[1,−6] ⇒ h_AB: x−6y+c=0 i 2−6*8+c=0 ⇒ ⇒ c=46 i x−6y+46=0, czyli h_AB: x−6y+46=0 − szukane równanie wysokości