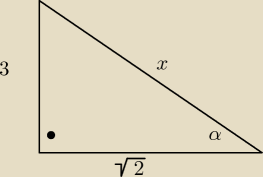
 Dla kąta ostrego z rysunku.
Dla dowolnego:
Dla kąta ostrego z rysunku.
Dla dowolnego:
| cosx | √2 | ||
= | i | ||
| sinx | 3 |
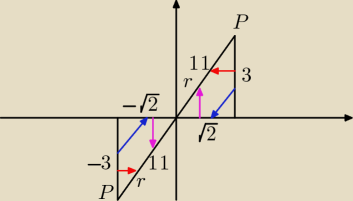 Krystku, sorry, ale dla dowolnego kąta też można zrobić geometrycznie. Po co sobie
komplikować życie układami równań, tam gdzie mozna rozwiązać zadanie na jednej niewiadomej?
Rysujesz układ oraz dwa trójkąty prostokątne (tg dodatni, więc I lub III ćw.), aby lepiej
zobrazować zadanie przy przyprostokątnych zamiast długości boków zaznaczasz wartości
współrzędnych wierzchołka P (dlatego mogą być one ujemne, bo to współrzędne, a nie dlugości)
jak na rysunku.
Potem obliczasz przeciwprostokątną r (promień wodzący) z Pitagorasa:
r2=(√2)2+32=2+9=11
i lecisz strzałeczkami z definicji funkcji trygon.
Krystku, sorry, ale dla dowolnego kąta też można zrobić geometrycznie. Po co sobie
komplikować życie układami równań, tam gdzie mozna rozwiązać zadanie na jednej niewiadomej?
Rysujesz układ oraz dwa trójkąty prostokątne (tg dodatni, więc I lub III ćw.), aby lepiej
zobrazować zadanie przy przyprostokątnych zamiast długości boków zaznaczasz wartości
współrzędnych wierzchołka P (dlatego mogą być one ujemne, bo to współrzędne, a nie dlugości)
jak na rysunku.
Potem obliczasz przeciwprostokątną r (promień wodzący) z Pitagorasa:
r2=(√2)2+32=2+9=11
i lecisz strzałeczkami z definicji funkcji trygon.
| 1 | 3 | 3√2 | ||||
tgα= | }= | = | w obu trójkątach tg jest dodatni (I i III ćw.) | |||
| ctgα | √2 | 2 |
| 3 | 3 | |||
sinα= | dla ćw. I lub sinα=− | dla ćw. III | ||
| 11 | 11 |
| √2 | √2 | |||
cosα= | dla ćw. I lub cosα=− | dla ćw. III | ||
| 11 | 11 |