ekstrema mikołaj: Znajdź największą i najmniejszą wartość funkcji f(x, y) = 2x² − 2y² w kole x² + y² ≤ 4.

Basia: f'_x = 4x f'_y = −4y jedyny możliwy punkt stacjonarny P(0,0) f"_xx = 4 f"_xy = 0 f"_yx = 0 f"_tt = −4 hesjan W = −16 < 0 czyli nie ma ekstremum lokalnego z tego wynika, że wartość największa (największa) może być tylko na brzegu obszaru x²+y² = 4 y² = 4−x² f(x,y) = 2x² − 8 + 2x² = 4x²−8 = 4r²*cos²β − 8 gdzie r=2 i β dowolne f(r,β) = 16cos²β − 8 0 ≤ cos²β ≤ 1 /*16 0 ≤ 16cos²β ≤ 16 /−8 −8 ≤ 16cos²β−8 ≤ 8 czyli f_min = −8 f_max = 8

mikołaj: bardzo dziękuję, mam jeszcze jedno zadanie, którego nie potrafie zrobić 1. Znajdź największą wartość funkcji f(x, y) = x²y − 8x − 4y w trójkącie domkniętym ograniczonym przez proste o równaniach x = 0, y = 0 i x + y − 4 = 0.

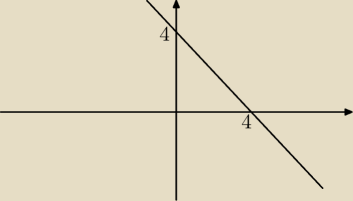
Basia: x≥0 i y≥0 i y≤−x+4 f'_x = 2xy − 8 f'_y = x² − 4 2xy −8 = 0 x²−4=0 (x−2)(x+2) = 0 x = −2 ⇒ −4y−8=0 ⇒ y=−2 nie spełnia warunków zadania lub x=2 ⇒ 4y−8=0 ⇒ y=2 spełnia warunki zadania f"_xx = 2y f"_xy = 2x f"_yx = 2x f"_yy = 0 W(x,y) = 2y*0 − 2x*2x = −4x² W(2,2) = −16<0 nie ma ekstremum lokalnego czyli znowu trzeba zbadać wartości na brzegu dla x=0 f(x,y) = −4y wartość największa dla y=0 czyli 0, najmniejsza dla y=4 czyli −16 dla y=0 f(x,y) = −8x wartość największa dla x=0 czyli 0, najmniejsza dla x=4 czyli −32 dla y= −x+4 f(x,y) = x²(−x+4)−8x−4(−x+4) = −x³ + 4x² − 8x + 4x −16 = −x³ + 4x² +4x − 16 f'_x = −3x² + 8x + 4 Δ = 64 − 4*(−3)*4 = 16(4+3) = 16*7 √Δ = 4√7

	−8−4√7		4+2√7
x1 =		=
	−6		3

pytanie czy to spełnia warunki zadania

4+2√7
	≤ 4 (?)
3

4+2√7 ≤ 12 2√7 ≤ 8 √7 ≤ 4 prawda

	4+2√7
0 ≤ −		+ 4 (?)
	3

	4+2√7
−4 ≤ −		/*(−3)
	3

12 ≥ 4+2√7 prawda

	−8+4√7		4−2√7
x2 =		=		< 0 nie spełnia warunków zadania
	−6		3

no to policz f_min= f(x,y) = −x³ + 4x² +4x − 16

	4+2√7
dla x=
	3

i wybierz wartość najmniejszą i największą z liczb: f_min i tych wyliczonych wcześniej czyli: 4, −16, −32

mikołaj: dzięki wielkie

Geseth: Witaj Basiu, przy podliczaniu po podstawieniu pod y (−x+4), dla 3−ciego brzegu wystąpił niewielki błąd: f(x,y) = x²(−x+4)−8x−4(−x+4) = −x³ + 4x² − 8x + 4x −16 = −x³ + 4x² +4x − 16 wynik powinien wygladać następująco: −x³ + 4x² − 4x − 16 (minus przed 4x zamiast plusa). Po uwzględnieniu tego nie ma większego problemu ze sprawdzaniem czy wyniki spełniają warunki zadania. Pozdrawiam