Udowodnij, że kąt ostry wyznaczony k.p: Udowodnij, że kąt ostry wyznaczony przez przekątne prostokąta ma miarę 2 razy większą od miary kąta, który tworzy przekątna z dłuższym bokiem prostokąta.

Mila: Skorzystaj z twierdzenia, że kąt zewnętrzny Δ jest równy sumie kątów wewnętrznych nie przyległych do niego. II sposób z sumy katow w Δ i sumy kątów przyległych.

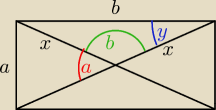
123: Oznaczenia: a = α b = β y = γ Rozwiązanie: β = 180^o − α // kąt półpełny

	180o − β		180o − (180o − α)		α
γ =		⇒ γ =		⇒ γ =		c.n.d.
	2		2		2

pigor: ... narysuj sobie prostokąt ABCD (AB>BC) i 2−ie jego przekątne przecinające się w punkcie O , który połącz z środkiem E boku np. BC (lub AD) , to połowa kąta ostrego BOC , np. kąty ∡ BOE = ∡ABO są równe jako kąty naprzemianległe wewnętrzne , czyli miary ¹₂∡BOC=∡ABO /*2 ⇔ ∡BOC=2∡ABO c.n.u. . ...