Dana jest funkcja f(x)= x^2+ ax + (1-b), określona w zbiorze liczb rzeczywistyc Lila: a) Dla a=0 i b=1 rozwiąż graficznie nierówność f(x) ≥ x+2 b) Wiedząc, że wykres funkcji f ma z osią OY punkt wspólny o współrzędnych (0;−3), zaś jednym z miejsc zerowych zerowych funkcji f jest liczba 5, ustal wartości współrzędnych a i b.

Lila:

Lila: jak tu zacząć?

Buuu: a) x²≥x+2 x²−x−2≥0 Δ=1+8=9

	1−3
x1=		=−1
	2

	1+3
x2=		=2
	2

Funkcja się uśmiecha, więc f(x)≥0 ⇔ x∊(−∞, −1>∪<2, ∞) b) 1−b = −3 ⇒ b = 4, bo to punk przecięcia z osią rzędnych, 5²+5a+(1−4)=0 5a=−22 a=4²₅

Lila: ale tą nierówność trzeba rozwiązać graficznie i bez równań kwadratowych

Buuu: x²≥x+2 x²−x−2≥0 x²+x−2x−2≥0 x(x+1)−2(x+1)≥0 (x−2)(x+1)≥0 I przyrównuję: (x−2)(x+1) = 0 x−2=0 v x+1=0 x=2 v x=−1 Proszszsz

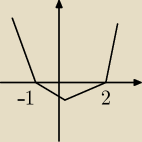
Buuu: Coś tu krzywe mi wycina.