biegunowe Soulja: Witam, przy obliczaniu całki podwójnej po obszarze normalnym którym jest koło zmieniamy współrzędne na biegunowe. Gdy środek okręgu jest w początku układu współrzędnych to nie ma problemu r zmienia się od 0 do R a fi od 0 do 2pi. Jak mamy okrąg " po lewej stronie" styczny do osi OY to mamy że fi zmienia się od −pi/2 do pi/2 a r zmienia się od 0 do Rcosfi. Gdy okrąg jest jakby na górze czy styczny do OX to fi zmienia się od 0 do pi ale jak zmienia się r Czy r też zmienia się od 0 do Rcosfi jak w przykładzie gdzie koło jest po lewej czy jest jakaś inna zależność ? pomóżcie bo utknąłem a w necie nie umiem znaleźć

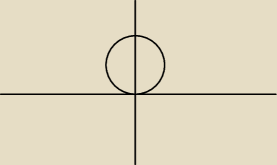
Soulja: chodzi mi o taki przypadek

Krzysiek: wszystko zależy w jaki sposób zmienisz zmienne np: w takim przypadku jak na rysunku możesz zastosować: x² +(y−R)² =R² x=rcosφ y=rsinφ +R i wtedy r∊[0,R]

Soulja: a jak zmienne zmienię w sposób "tradycyjny" czyli : x=rcosφ y=rsinφ to jak będzie zmieniało się moje r ?

Krzysiek: wstaw do równania okręgu i sprawdź Sam/a

Soulja: r[0; 2Rsinφ ] DZIĘKI WIELKIE