Uklad wspolrzednych MarekPaslek: blicz pole czworokąta o podanych wierzchołkach: A(1,5), B(2,4), C(4,51), D(3,81).

milord: up

ZKS: Sposób z geodezji x_n| y_n | y_{n + 1} − y_{n − 1}| x_n(y_{n + 1} − y_{n − 1}) 1 5 −77 −77 2 4 46 92 4 51 77 308 3 81 −46 −138 ∑ = 0 ∑ = 2P

	185
2P = −77 + 92 + 308 − 138 ⇒ 2P = 185 ⇒ P =
	2

pigor: ... "widzę" ten czworokąt i jego pole np. tak : P= 3*(81−4)−¹₂[1*1+2*(51−4)+1*(81−51)+2*(8−5)]= = 3*77−¹₂(1+2*47+30+2*76)= 231−¹₂(31+94+152)= = 231−¹₂*277= 231−138,5=92,5 j² . ...

MarekPaslek: Ale mam do wyboru 109 Wybierz B 98,23 Wybierz C 120 Wybierz D 121,5 Wybierz E 68 Wybierz F 115 Wybierz

ZKS:

	185
Przecież widzisz jaka jest odpowiedź		= 92.5 więc sprawdź czy Ty nie przepisałeś
	2

jakiejś współrzędnej źle.

MarekPaslek: Widze, i odpowiedzi sa dobre.

ZKS: To jak zgadza się?

Warszawiak: Właśnie nie, a odpowiedzi są dobre

MarekPaslek: Widze, ze kolega też robi zadanka podlaczam sie, odpowiedzi sa dobre

ZKS: To trzeba dopisać odpowiedź G 92.5.

Basia: policzcie to normalnie P = P_tr.ABD+P_tr.BCD = ¹₂|d(AB^→;AD^→)| + ¹₂|d(BC^→;BD^→)| teraz może Warszawiak i Marek policzą sami 1. współrzędne tych wektorów 2. wyznaczniki par wektorów czyli u₁*v₂ − u₂*v₁ 3. podstawią do podanego wzoru

MarekPaslek: co ma oznaczac d ?

MarekPaslek: AB − 4,213 AD − 76,026 BC− 47,042 CD − 30,1 źle ?

Gustlik: Posłuchaj rady Basi: podziel przekątną ten czworokąt na dwa trójkąty i jedź z wyznacznika wektorów − tu masz to wyjaśnione: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18

Basia: wyznacznik pary wektorów jeżeli u^→ = [u₁;u₂] v^→ = [v₁;v₂] to d(u^→;v^→) = u₁*v₂ − u₂*v₁ stąd się wzięła nazwa to jest wyznacznik macierzy (u₁ u₂) (v₁ v₂)

pigor: ... to jest tylko oznaczenie wyznacznika (od determinant) . ...

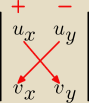
Gustlik: u^→=[u_x, u_y] v^→=[v_x, v_y] det(u^→, v^→)=u_x*v_y−u_y*v_x Na rysunku pokazałem, jak się liczy wyznacznik: na krzyż − pierwsza przekątna minus druga przekątna. Proste jak drut.

pigor: ...MarkuPasiek , jeszcze ja zapytam, czy na pewno "twoje" współrzędne wierzchołków danego czworokąta są takie jakie powinny być , co

ZKS: I ja dołączam się do pytania które zadał pigor.

pigor: .., nie wstydź się przyznać MarkuP, bo mało prawdopodobne abyśmy licząc "twoje" pole różnymi metodami i otrzymując takie same wyniki ... nie mieli racji

ZKS: Jednak do czegoś mi się przydaje geodezja.

Basia: mnie też wyszło 92,5

ZKS: Więc 3 osobom wyszły takie same wyniki.

MarekPaslek: A(1,5), B(2,4), C(4,51), D(3,81) ,współrzędne są dobrze . A nie można poprostu policzyć długości odcinków, jedną przekątną i poliyczć pola powstałych trójkątów ze wzoru Herona ?

Ajtek: Można i wynik zapewne wyjdzie 92,5.

MarekPaslek: Zaraz policze tym sposobem , zaraz sprawdzę.

MarekPaslek: Wyszło ok. 92,016 przybliżając niektóre liczby

Ajtek: Dlatego tutaj wzór Herona jest nieprzydatny. Przeanalizuj rozwiazania pokazane wyzej . Ewentualnie nie przybliżaj, tylko w wyniku obliczeń powinny ładnie się zredukować.

MarekPaslek: Chcialem poprostu zrobić to sposobem banalnym

pigor: hmm ... banalny sposób to jest mój, bo od pola prostokąta "opisanego" na danym czworokącie odejmujesz pola 4−ech trójkątów prostokątnych o kątach prostych w jego "rogach" (wierzchołkach)...