Teoria równania kwadratowego ;)
V.Abel: Dane jest równanie kwadratowe ax2+bx+c, gdzie a jest współczynnikiem kwadratowym infornującym
nas o ramionach(góra/dół; strzelistość) wyraz wolny c(pokazuje przecięcie z osią OY) oraz
współczynnik liniowy b. Moje pytanie brzmi:
dlaczego b jest nazwany współczynnikiem liniowym(co za tym idzie)? oraz gdzie on jest na
wykresie? ...
6 cze 15:14
konrad: od współczynnika b zależy przesunięcie wykresu wzdłuż osi x
to tyle co wiem

6 cze 15:24
V.Abel: czyżby? czy tylko? czy na pewno?
6 cze 15:35
konrad: na pewno ale czy tylko to nie wiem
6 cze 15:42
krystek: Nie ! o przesunięciu wyliczone pi q , postac kanoniczna
y=a(x−p)2+q
6 cze 17:37
konrad: ale wpływ ma
6 cze 17:41
Basia: Witaj
krystek 
w pewnym sensie jednak
tak;
dla b=0 wierzchołek paraboli
leży na osi OY
dla b≠0 wierzchołek paraboli
nie leży na osi OY
nic więcej nie da się o
samym b powiedzieć
6 cze 17:43
V.Abel: "zmiana b powoduje zachowanie punktu przecięcia z osią OY przy jednoczesnym przesuwaniu
paraboli zgodnie ze zwrotem OX, jeżeli b < 0 i przeciwnie do niego, jeżeli b > 0; "
tak napisała Wikipedia

to czyli, jak się zmienia b przy zachowaniu stałych współczynników a i c, to wierzchołek
przesuwa się do funkcji przeciwnej do pierwotnej

chyba

tylko dlaczego on się nazywa
liniowym ? ? ?
6 cze 23:11
V.Abel: nie "do" tylko "po"

Jeszcze takie pytanie :
mam dwa okręgi O
1 : (0,0) r=
√10 oraz O
2:(3,3)r=2. Oblicz długość wspólnej cięciwy

?
Jak...
6 cze 23:16
Basia:
daj link, poprawię bo to co cytujesz jest prawdą tylko dla a>0
dla a<0 jest akurat odwrotnie
a dlaczego liniowy to zrozumiesz jak sobie narysujesz (jeden rysunek) wykresy np:
y = x2 − 4
y = x2 − 4x − 4
y = x2 + 8x − 4
albo
y = −x2+4
y = −x2+4x+4
y = −x2−8x+4
albo jeszcze jakieś inne (a,c takie same; zmieniasz sobie b i patrzysz co się dzieje)
6 cze 23:18
Basia:
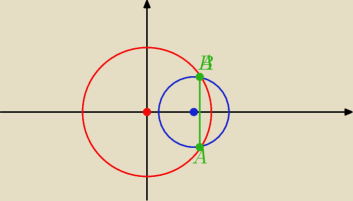
wspólna cięciwa to odcinek AB
trzeba znaleźć współrzędne A i B i policzyć jego długość
A i B są punktami wspólnymi obu okręgów
wiesz jak się szuka punktów wspólnych ?
6 cze 23:23
Basia:
2 sposób
szukasz takich punktów P(x,y) dla których
|O1P| = √10
|O2P| = 2
6 cze 23:25
6 cze 23:26
V.Abel: no właśnie jak znaleźć punkty wspólne

?
6 cze 23:28
Basia:
źle; ale to nie ma znaczenia
6 cze 23:28
Basia:
układ równań, tylko trzeba napisać najpierw równania okręgów
drugi sposób jest prostszy i szybszy
6 cze 23:29
V.Abel: ok

a z trójkąt mogę? tak że odległość pkt od środka(3,3) jest równa 2 potem odległość tego
środka od odcinka szukanej cięciwy, i potem z Pitagorasa ? ? ?
6 cze 23:34
V.Abel: a właściwie to wychodzi Ci może 2
√3, jeśli liczyłaś

?..
6 cze 23:38
Basia: wcale nie liczyłam; napisz jak Ty liczyłeś to sprawdzę
6 cze 23:43
V.Abel: Równanie pierwszego okręgu mam (x−3)
2 +(y−3)
2 =4 a drugiego x
2+y
2 =10 zrobiłem układ
równań i heh.. mam deltę ujemną, więc tak średnio, pewnie coś gdzieś nie tak policzyłem,
chociaż...
Ale wyżej napisałeś o trójkącie, można w taki " mój" sposób

? ..
6 cze 23:45
Basia: wynik masz dobry AB = 2√3
6 cze 23:46
V.Abel: ok, ale co z tym równaniem ? ..
6 cze 23:47
Basia:
zacząłeś dobrze
no to mamy
x2+y2=10
x2 − 6x + 9 + y2 − 6y + 9 = 4
10 − 6x − 6y +18 = 4
28 − 4 − 6x = 6y
6y = 24 − 6x / :6
y = 4 − x
x2+(4−x)2 = 10
x2+16−8x+x2−10 = 0
2x2 − 8x + 6 = 0 / :2
x2 − 4x + 3 = 0
licz dalej
6 cze 23:51
V.Abel: ok jest późno 24/6=4 a nie 6

dzięki Basia

Czy oprócz tych dwóch sposobów, które mi napisałaś istnieją jeszcze jakieś możliwości
wyliczenia tego ? ? ?
6 cze 23:55
Basia:
jak się człowiek uprze, to pewnie jeszcze jakiś znajdzie
mnie już żaden inny nie przychodzi do głowy
6 cze 23:57
V.Abel: Ale właściwie ten drugi sposób z szukaniem p−któw sprowadza się do tego samego, tak ?..
6 cze 23:57
V.Abel: Spoko

dzięki za pomoc

Mam wrażenie, że jesteś rozdrażniona, późno jest

..
6 cze 23:59
Artur z miasta Neptuna:
tak ... właściwie się sprowadza do tego samego
7 cze 00:01
Basia:
dokładnie do tego samego
7 cze 00:04
Basia: to nie rozdrażnienie; po prostu tak jest, że jak się człowiek uprze to wymyśli jeszcze kilka
sposobów
(czasem dosyć dziwacznych i karkołomnych)
ale naprawdę żaden mi teraz nie przychodzi do głowy, nawet taki cudaczny
7 cze 00:06
V.Abel: Ok, dziękuję Wam bardzo, jtr jeszcze wrzucę jedno zadanko. Dobrej nocy

7 cze 00:06
Mila:
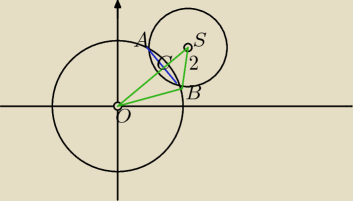
|OS|=3
√2
|SB|=2
|OB|=
√10
1) w ΔSBO − Z tw. cosinusów obliczamy cos <OSB
2) Obliczamy |CB| w ΔSCB
7 cze 13:18
V.Abel: Mila, ale jak z trójkąta SCB ? .. (Ja to z pola SOB zrobiłem)
7 cze 18:58
Mila: Jakie masz to pole i jak go obliczyłeś?
Oblicz cosinus kąta OSB i podaj.
8 cze 16:21
V.Abel: Zrobiłem najpierw wg tego, co mówiła Basia.Uznałem wynik za dobry. Wtedy zacząłem liczyć wg
Twojego pomysłu, ale nie wiedziałem do końca dlaczego napisałaś ΔSCB, więc zrobiłem tak:
1) Z tw.cos. :
18= 10+4− 2*2*√10*cosγ
cosγ ≈0,3162, dokładnie −√1010, czyli γ≈108 ◯ (jak tu się robi " stopnie kątów" ?..)
Potem : P=12absinγ
P=3[j2]
P=12ab
3=3√2* |CB|2
|CB|=√2 ==> |AB|=2√2
Powiesz, o co chodzi z tym ΔSCB ?.. Proszę...
8 cze 22:50
Mila:
Problem polega na tym, że obliczyłeś cosinus innego kąta.(nieuwaga?)
|OB|
2=|OS|
2+|SB|
2−2*|OS|*|SB|*cosγ
10=18+4−2*2*3
√2*cosγ
10=22−12
√2cosγ
−12=−12
√2cosγ
γ=45
0
czyli SC=SB=
√2
AB=2
√2
8 cze 23:15
V.Abel: jak to ? ale ja wziąłem |OS|2=|OB|2+|SB|2−2...cosγ
8 cze 23:18
Mila: Twój kąt ma wierzchołek B a mój S.
O różnych kątach pisaliśmy.
8 cze 23:23
V.Abel: OK, racja

, grunt, że wyszedł ten sam wynik.. Dziękuję za pomoc

8 cze 23:24
Mila: Tak, ąle mój sposób, po obliczeniu cosinusa ma dwie linijki, a czas to pieniądz.
8 cze 23:26
V.Abel: Prawda

W ogóle zawsze masz "trafne"(pod wieloma względami) rozwiązania

.Nie umniejszając
przy tym innym

8 cze 23:38
Mila: Dzięki za dobre słowo. Często piszę i nie wiem, czy to ktoś to czyta.
Rozwiązuj zadania.
8 cze 23:41
picia: czyta, czyta

8 cze 23:43
V.Abel: Ja czytam

// A Ty dużo liczysz? Czy po prostu jesteś "genialna" i lubisz pomogać takim jak
ja

na forum ?..
8 cze 23:44
Mila: Myślę, że jestem uzależniona od miłych osób pomagających i tych, którzy potrzebują pomocy.

9 cze 23:37

 w pewnym sensie jednak tak;
dla b=0 wierzchołek paraboli leży na osi OY
dla b≠0 wierzchołek paraboli nie leży na osi OY
nic więcej nie da się o samym b powiedzieć
w pewnym sensie jednak tak;
dla b=0 wierzchołek paraboli leży na osi OY
dla b≠0 wierzchołek paraboli nie leży na osi OY
nic więcej nie da się o samym b powiedzieć
 to czyli, jak się zmienia b przy zachowaniu stałych współczynników a i c, to wierzchołek
przesuwa się do funkcji przeciwnej do pierwotnej
to czyli, jak się zmienia b przy zachowaniu stałych współczynników a i c, to wierzchołek
przesuwa się do funkcji przeciwnej do pierwotnej  chyba
chyba  tylko dlaczego on się nazywa liniowym ? ? ?
tylko dlaczego on się nazywa liniowym ? ? ?
 Jeszcze takie pytanie :
mam dwa okręgi O1 : (0,0) r=√10 oraz O2:(3,3)r=2. Oblicz długość wspólnej cięciwy
Jeszcze takie pytanie :
mam dwa okręgi O1 : (0,0) r=√10 oraz O2:(3,3)r=2. Oblicz długość wspólnej cięciwy  ?
Jak...
?
Jak...
 wspólna cięciwa to odcinek AB
trzeba znaleźć współrzędne A i B i policzyć jego długość
A i B są punktami wspólnymi obu okręgów
wiesz jak się szuka punktów wspólnych ?
wspólna cięciwa to odcinek AB
trzeba znaleźć współrzędne A i B i policzyć jego długość
A i B są punktami wspólnymi obu okręgów
wiesz jak się szuka punktów wspólnych ?
 ?
?
 a z trójkąt mogę? tak że odległość pkt od środka(3,3) jest równa 2 potem odległość tego
środka od odcinka szukanej cięciwy, i potem z Pitagorasa ? ? ?
a z trójkąt mogę? tak że odległość pkt od środka(3,3) jest równa 2 potem odległość tego
środka od odcinka szukanej cięciwy, i potem z Pitagorasa ? ? ?
 ?..
?..
 ? ..
? ..
 dzięki Basia
dzięki Basia  Czy oprócz tych dwóch sposobów, które mi napisałaś istnieją jeszcze jakieś możliwości
wyliczenia tego ? ? ?
Czy oprócz tych dwóch sposobów, które mi napisałaś istnieją jeszcze jakieś możliwości
wyliczenia tego ? ? ?
 dzięki za pomoc
dzięki za pomoc  Mam wrażenie, że jesteś rozdrażniona, późno jest
Mam wrażenie, że jesteś rozdrażniona, późno jest  ..
..

 |OS|=3√2
|SB|=2
|OB|=√10
1) w ΔSBO − Z tw. cosinusów obliczamy cos <OSB
2) Obliczamy |CB| w ΔSCB
|OS|=3√2
|SB|=2
|OB|=√10
1) w ΔSBO − Z tw. cosinusów obliczamy cos <OSB
2) Obliczamy |CB| w ΔSCB
 , grunt, że wyszedł ten sam wynik.. Dziękuję za pomoc
, grunt, że wyszedł ten sam wynik.. Dziękuję za pomoc 
 W ogóle zawsze masz "trafne"(pod wieloma względami) rozwiązania
W ogóle zawsze masz "trafne"(pod wieloma względami) rozwiązania  .Nie umniejszając
przy tym innym
.Nie umniejszając
przy tym innym 

 // A Ty dużo liczysz? Czy po prostu jesteś "genialna" i lubisz pomogać takim jak
ja
// A Ty dużo liczysz? Czy po prostu jesteś "genialna" i lubisz pomogać takim jak
ja  na forum ?..
na forum ?..
