Trygonometria Jurek: Oblicz wartości funkcji trygonometrycznych kąta ostrego α, wiedząc, że zachodzi podana zależność: a) sin²α − cos²α=1/2 b)tgα=3ctgα

Jurek: Wie ktoś może? Kompletnie nie wiem jak się za to zabrać

Eta:

	1
a) 1−cos2α−cos2α=
	2

	1
2cos2α=
	2

	1
cos2α=		to dla kąta ostrego
	4

	1
cosα=		⇒ α= 60o
	2

sin60^o=... tg60^o=.... ctg60^o=...

	3
b) tgα=		⇒ tg2α= 3 ⇒ tgα=√3 ⇒ α= 60o
	tgα

sin60^o=... cos60^o=... ctg60^o=....

Buuu: a)

⎧	sin2α − cos2α = 0,5
⎩	sin2α + cos2α =1

Dodaj stronami b) tg*ctg =1

Jurek: Nie rozumiem przykładu a) skąd się nagle wzięło 1−cos²−cos²=1/2 ? skąd?

picia: https://matematykaszkolna.pl/strona/450.html

Eta: Żal,że nie rozumiesz sin²α+cos²α=1 −−−− jedynka trygonometryczna to sin²α= 1−cos²α

Jurek: Okej, już wiem. Jeszcze mam jeden przykład... c) 4tgα − 3sin²α = 3cos²α teraz trudniej

Buuu: 4tgα = 3cos²α + 3sin²α 4tgα = 3(cos²α + sin²α) 4tgα=3 tgα=³₄

Jurek: wyszedł mi α=37 stopni, dobrze?

Jurek: wyszedł mi α=37 stopni, dobrze?

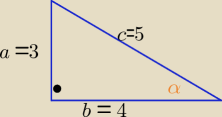
Eta: 4tgα= 3sin²α+3cos²α 4tgα= 3(sin²α+cos²α) 4tgα= 3*1

	3		a
tgα=		=		a= 3 b= 4 c2= 32+42 ⇒ c= 5
	4		b

	4
ctgα=
	3

	a
sinα=		=...
	c

	b
cosα=		=....
	c

Jurek: Bardzo dziękuję

Eta: Na zdrowie