zad Patrycja: Punkty A(0,3) i B(4,5) są wierzchołkami trójkąta równoramiennego ABC, w którym |AB|=|BC| Wysokość BD trójkąta zawira sie w prostej o równaniu 3x−y−7=0 oblicz: a) współrzędne wierzchołka C

tim: 1. Narysuj sobie odcienek AB. 2. Narysuj sobie prostą 3x − y − 7 = 0 → y = 3x − 7 3. Znajdź wzór prostej AC prostopadłej do wysokości ↑. 4. Dorysuj lustrzane odbicie trójkąta ABD względem prostej BD . Wyjdzie ci C.

Patrycja: Wszystko mam tylko nie wiem jak obliczyc wspolrzedne wierzcholka C Ułorzyłam układ równań i prostąBD i Ac i zamiast wyjsc mi punkt C to wyszeld D Jak dalej

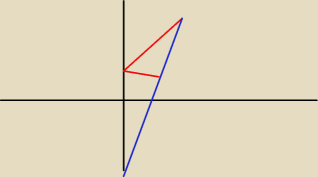
tim: Masz coś takiego? czerwone − boki, niebieska − wysokość?

Patrycja: Zgadza sie

Patrycja: rownanie prostej prostopadlej do wysokosci my=−¹₃x + 3

tim: No. To teraz Wierzchołek C zawiera się w prostej o równaniu

	1
y= −		x+3 zaś odległość |AB|=2√5 zatem punkt C ma współrzędne
	3

	1
C(x;−		x+3)
	3

wykorzystaj długość |AB| 2√5= √(4−x)²+(5+ ¹₃x−3)² Wyznaczysz x.

Patrycja: Skąd wiesz że |AB|=2√5?

tim: https://matematykaszkolna.pl/strona/1248.html