Prziałał funkcji Wera: Na jakim przedziale funkcja f(x) =x²lnx jest wypukła a na jakim wklęsła ?

Artur_z_miasta_Neptuna: liczysz druga pochodną i przyrównujesz ja do zera wklęsła gdy f''>0 wypukła gdy f''<0

Patronus: musisz policzyć drugą pochodną:

	1
f'(x) = 2xlnx + x2*		= 2xlnx + x
	x

	1
f''(x) = 2lnx + 2x*		+ 1 = 2lnx + 3
	x

i teraz dla f''(x)<0 funkcja jest wypukła i f''(x)>0 jest wklęsła

Wera: a jak obliczyć lnX ?

konrad: tzn ?

Wera: no nie wiem jak to przyrównać do zera co mi wyszło z 2 pochodnej, żeby zobaczyć w jakim przedziale rośnie a w jakim maleje

konrad: 2lnx+3=0 2lnx=−3 lnx=−3/2 x=e^−3/2

konrad: lub x=√e⁻³

Wera: czyli nie da się obliczyć przedziału wklęsłości i wypukłoości ?

Wera: halo jak wyliczyć wypukłość i wklęsłość tej funkcji. ;>

Artur_z_miasta_Neptuna: no jak się nie da wyliczyć? ile Ci wyszła druga pochodna? 2ln x + 3 No to liczysz: 2ln x + 3 = 0

	3
lnx = −
	2

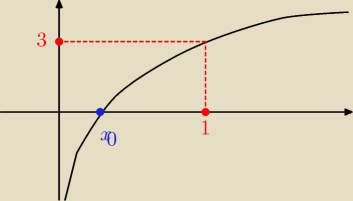
x = e^−3/₂ robisz szkic wykresu 2lnx + 3 ... (miejsce zerowe w x = e^−3/₂ ... a reszta to tak jak zwykły lnx) i już widzisz gdzie f'' jest >0 a gdzie <0