maturalne
on: na prostej l;x+y−6=0 wyznacz taki punkt C , aby dlugosc lamanej ACB, gdzie A (1,3) B(2,2)
bylanajmniejsza. uzasadnij swoje rozumowanie.
chodzi mi o to dla jakiesgo warunku to dlugosc bedzie najmniejsza
27 kwi 23:53
@Basia: Pomagam
27 kwi 23:58
kamil: to super
27 kwi 23:59
@Basia:
C(x,y) C∈l ⇒ y=−x+6 ⇒ C(x, −x+6)
AC = √(x−1)2 + (−x+6−3)2 = √(x−1)2 + (3−x)2
BC = √(x−2)2 + (−x+6−2)2 = √(x−2)2 + (4−x)2
zasadniczo f(x) = AC+BC
ale ponieważ AC>0 i BC>0
można zbadać
g(x) = AC2 + BC2
g(x) = (x−1)2 + (3−x)2 + (x−2)2 + (4−x)2
popodnoś do kwadratu, zredukuj wyrazy podobne i znajdź minimum
28 kwi 00:04
kamil: hmmm... chodzilo mi tylko o to zebys powiedziala mi co na;ezy zalozyc. tak jak np
najmnejsza odleglosc punktu od prostjj nalezy do prostej prostopadlej do danej. cos w
tym stylu. bo z tego zapisu nie wiem czego szukac. ale wielkie dzieki,i sorki za zle
sformulowane pytanie
28 kwi 00:09
@Basia: A po co ? Po wykonaniu działań dostaniesz zwykłą funkcję kwadratową.
Na pewno wiesz jak się szuka największej (najmniejszej) wartości f.kwadratowej.
28 kwi 00:15
kamil: dlaczego wole dociekac do tego? bo a noz widelec trafi sie cos pdobnego na maturze i
chcialbym iwedziec co nalezy zrobic a nie w glowie sobie przypominac co mi
podpowiedzialas.
28 kwi 00:18
@Basia: Ja tu korzystam tylko z wzorów na odległość punktów. Z niczego więcej.
Można udowodnić, że ten punkt to punkt przecięcia symetralnej odc.AB z prostą l.
Wtedy trzeba napisać równanie pr.AB
Znaleźć S − środek odc.AB
Napisać równanie pr.m prostopadłej do pr.AB
Znaleźć punkt wspólny pr.m i pr.l
28 kwi 00:29
kamil: no fanktycznie mozna tak zrobic i latwo wyjasnic, wlasnie o takie cos mi chodzilo
dzieki bardzo i milych snow zycze
28 kwi 00:47
@Basia: Dobranoc i powodzenia na maturze !
28 kwi 00:49
Bogdan:
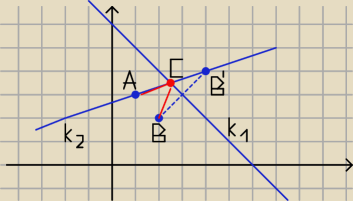
Proponuję takie rozwiązanie:
Tworzymy obraz jednego z punktów: A lub B w symetrii osiowej względem prostej
k
1: y = −x + 6, np. punktu B.
B = (2, 2), B' = (4, 4).
Łączymy punkty A i B' prostą k
2: y = ax + b.
A = (1, 3)
| | 1 | | 1 | | 1 | | 8 | |
a = |
| , k2: y − 3 = |
| (x − 1) => y = |
| x + |
| |
| | 3 | | 3 | | 3 | | 3 | |
Szukany punkt C jest punktem wspólnym prostej k
1 i prostej k
2.
|CB'| = |CB|
| | 1 | | 8 | | 5 | | 7 | |
y = −x + 6 i y = |
| x + |
| => x = |
| i y = |
| |
| | 3 | | 3 | | 2 | | 2 | |
28 kwi 01:41
Grzesiu Białek: @Basia: "Można udowodnić, że ten punkt to punkt przecięcia symetralnej odc.AB z prostą l.
Wtedy trzeba napisać równanie pr.AB
Znaleźć S − środek odc.AB
Napisać równanie pr.m prostopadłej do pr.AB
Znaleźć punkt wspólny pr.m i pr.l"
Czy przypadkiem nie jest to prawdziwe tylko wtedy, gdy odcinek AB jest równoległy do prostej?
15 kwi 21:26