 2x−y−4=0, x+2y−12= 0 i x−2=0
ad a)
Liczę współrzędne punktu A:
{ 2x−y−4=0
{ x+2y−12= 0
{ 2x−y=4 /*2
{ x+2y=12
{ 4x−2y=8
{ x+2y=12 +
−−−−−−−−−−−−−−−−−−−−−−−−−−
5x =20 /:5
x =4
4+2y=12
2y=12−4
2y=8 /:2
y=4
A=(4, 4)
Współrzędne B:
{ 2x−y−4=0
{ x−2=0 ⇒ x=2
2*2−y−4=0
4−y−4=0
−y=0
y=0
B=(2, 0)
Współrzędne C:
{ x+2y−12=0
{ x−2=0 ⇒ x=2
2+2y−12=0
2y=10 /:2
y=5
C=(2, 5)
A=(4, 4)
B=(2, 0)
C=(2, 5)
ad b) z wektorów:
AB→=[2−4, 0−4]=[−2, −4]
AC→=[2−4, 5−4]=[−2, 1]
BC→=[2−2, 5−0]=[0, 5]
|AB|=√(−2)2+(−4)2=√4+16=√20=2√5
|AC|=√(−2)2+12=√4+1=√5
|BC|=√02+52=5
obw=3√5+5
ad c)
A=(4, 4)
B=(2, 0)
C=(2, 5)
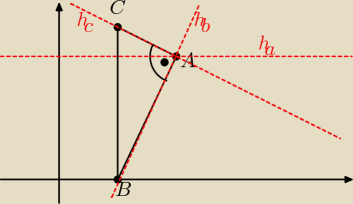
prosta hc ⊥ AB
2x−y−4=0, x+2y−12= 0 i x−2=0
ad a)
Liczę współrzędne punktu A:
{ 2x−y−4=0
{ x+2y−12= 0
{ 2x−y=4 /*2
{ x+2y=12
{ 4x−2y=8
{ x+2y=12 +
−−−−−−−−−−−−−−−−−−−−−−−−−−
5x =20 /:5
x =4
4+2y=12
2y=12−4
2y=8 /:2
y=4
A=(4, 4)
Współrzędne B:
{ 2x−y−4=0
{ x−2=0 ⇒ x=2
2*2−y−4=0
4−y−4=0
−y=0
y=0
B=(2, 0)
Współrzędne C:
{ x+2y−12=0
{ x−2=0 ⇒ x=2
2+2y−12=0
2y=10 /:2
y=5
C=(2, 5)
A=(4, 4)
B=(2, 0)
C=(2, 5)
ad b) z wektorów:
AB→=[2−4, 0−4]=[−2, −4]
AC→=[2−4, 5−4]=[−2, 1]
BC→=[2−2, 5−0]=[0, 5]
|AB|=√(−2)2+(−4)2=√4+16=√20=2√5
|AC|=√(−2)2+12=√4+1=√5
|BC|=√02+52=5
obw=3√5+5
ad c)
A=(4, 4)
B=(2, 0)
C=(2, 5)
prosta hc ⊥ AB
| wy | ||
a= | , gdzie [wx, wy] to współrzędne wektora leżącego na danej prostej lub | |
| wx |
| −4 | ||
aAB= | =2 | |
| −2 |
| 1 | ||
ahc=− | ||
| 2 |
| 1 | ||
y=− | x+b | |
| 2 |
| 1 | ||
5=− | *2+b | |
| 2 |
| 1 | ||
pr. hc: y=− | x+6 | |
| 2 |
| 1 | 1 | |||
aAC= | =− | (⊥ AB ⇒ Δ prostokątny) | ||
| −2 | 2 |
| 5 | ||
aBC= | nie istnieje | |
| 0 |