W prostokącie o przekątnej długości 12cm ania : ): W prostokącie o przekątnej długości 12cm połączono odcinkami środki sąsiednich boków. Otrzymany romb ma kąt ostry 60*. Oblicz obwód i pole tego rombu.

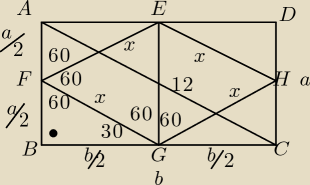
kuzynka: kąt ostry w rombie=60, więc kąty BFG i AFG są sobie = i wynoszą po 60 st., bo ^{180−60−60}₂ Suma kątów w rombie=360, więc kąty FGH i FEH= 120 st, czyli kąt EGF =60. z tego wynika, że trójkąty EFG i EGH są równoboczne, więc x=a, bo EG=a. Można też wyliczyć tę długość np. z tw. Talesa Z twierdzenia Talesa:

a/2		x
	=
a		12

	a/2* 12
x=
	a

x = 6 Obwód rombu U= 4*x= 4*6= 24, Z tw. Pitagorasa dla trójkąta ABC a² +b² =12² b²=144−a² b²=144−36=108 b=√108= √36*3=6√3

	1		1		1
Pole rombu p=		FH*EG=		a*b=		*6*6√3=18√3
	2		2		2

Aga1.: lub

	√3
P=x2*sin600=36*		=18√3.
	2