logiczne myslenie nonie: Udowodnic,ze w dowolnej grupie osob istnieją osoby o tej samej liczbie znajomych (w tej grupie).

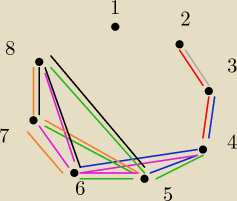
Artur_z_miasta_Neptuna: przykład dla n=8

Artur_z_miasta_Neptuna: dowód 'intuicyjny' (niewprost) Niech osoba 1 nie zna żadnej osoby. Wtedy osoba 2 MUSI znać przynajmniej jedną osobę (niech to będzie osoba '3'). W takim razie ta osoba zna '2' ... więc MUSI znać jeszcze kogoś innego (niech to będzie '4'). W takim razie '4' zna '3' ... musi więc znać jeszcze minimum dwie osoby ('5' i '6'). '5' i '6' znają '4', więc muszą znać jeszcze minimum trzy i cztery osoby ... itd. dojdzie do tego, że osoba 'n' (ostatnia) będzie musiała znać minimum 'n−1' osób (czyli wszystkie w grupie) ale nie może ich znać bo założyliśmy, ze osoba '1' nie zna nikogo z grupy. Sprzeczne Załóżmy, że w grupie nie ma osoby, która nie zna żadnej innej osoby z grupy. W takim razie jest w gronie osoba która musi znać minimum 1 osobę. Inna osoba musi znać minimum dwie. Itd. W końcu dochodzimy do sytuacji, że musi być w grupie (n osób) osoba, która będzie znała minimum n osób. Co jest nierealne ... bo może znac maksymalnie 'n−1' osób. Sprzeczne