Zadanie Godzio: Trivial albo Krzysiek jesteście może dostępni ?

Godzio: albo Basia ?

Godzio: Obliczyć objętość bryły ograniczonej powierzchniami z = 3(x² + y²) , z = 4 − √x² + y² Mógłby to ktoś zrobić, bardzo potrzebuję na teraz, będę bardzo wdzięczny

Krzysiek: jak dla mnie to będzie coś takiego: (na biegunowe) http://www.wolframalpha.com/input/?i=%7Bz%3D3r%5E2+%2C+z%3D4-sqrt%28r%5E2+%29+%7D ∫₀^2π dφ ∫₀¹ (4−√r² −3r² )r dr

Godzio: A mógłbyś to trochę rozpisać, pomagam koleżance i chciałbym, żeby miała to dobrze

Krzysiek: po przejściu na biegunowe mamy: z=3r² z=4−√r² po zrzutowaniu na płaszczyznę OXY otrzymujemy okrąg o promieniu 1(jak porównamy obie funkcję to otrzymamy r=+/− 1 ) zatem granice całkowania już znamy i patrzymy na funkcje która jest 'nad' drugą funkcją. widać, że z₁=4−√r² jest 'nad' z₂=3r² (dla r∊[0,1] ) zatem jakobian: |J|=r ∫₀^2π dφ ∫₀¹ (z₁ −z₂ )r dr

Godzio: Ok, dzięki

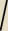
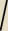Upewnij się, że wartość wyraże: (x² − 3 )² − (x − 2 )(x² + 4 )