długość trzeciego boku Oleńka :D: dwa boki trójkąta mają długości √29 i 5√2, akąt przeciwległy krótszemu z nich ma miarę 45 stopni. Oblicz długość trzeciego boku trójkąta

lisek: rozwiązuje

Bogdan: Zastosuj wzór kosinusów.

♊: Bogdan: A to przypadkiem twierdzenie nie jest ? ;P

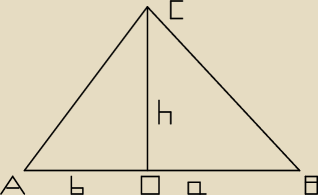
lisek: |AC|=√29 |BC|=5√2 |AD|=b |DB|=a |CD|=h Z ΔCDB:

	h
sin45=
	5√2

h=a=5 Z ΔADC i tw. Pitagorasa: b²=29−25 b=2 |AB|=a+b=7

Bogdan: II − o jakim twierdzeniu mówisz? Bo jeśli chodzi o użyte przez mnie sformułowanie, to można powiedzieć: "wzór kosinusów", "twierdzenie kosinusów", "twierdzenie Carnota". W tym zadaniu: |AB| = c i √c² + √29 > √50 (warunek trójkąta) Stosując wzór kosinusów otrzymujemy:

	√2
29 = 50 + c2 − 10c√2*		=> c2 − 10c + 21 = 0, Δ = 16
	2

c = 3 (nie spełnia warunków zadania) lub c = 7

♊: Dokładnie o twierdzenie Carnot'a mi chodziło, pierwszy raz się spotkałem z frazą "wzór kosinusów".

Bogdan: A jak częściej mówimy: wzór sinusów, czy wzór Snelliusa? Przez analogię używa się sformułowania "wzór kosinusów", np. tu: http://pl.wikipedia.org/wiki/Twierdzenie_cosinus%C3%B3w http://www.matematyk.edu.pl/czytaj-art-42.html http://www.zgapa.pl/zgapedia/Wz%C3%B3r_cosinus%C3%B3w.html

marta: hej mam zadanko .pomożcie mi je rozwiązaćblicz pole rombu o boku 17cm, w którym długości przekątnych różnią się o 14 cm.