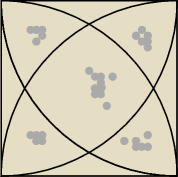
planimetria w wersji hard Ada: Bok kwadratu równa się 20cm. oblicz pole "zacieniowanej" figury

Ada: nie ma nikogo chętnego do pomocy ?

Maslanek: To prawdziwa wersja hard

Ada: 100π 1/4 tego koła, 400cm sq pole tego kwadratu, długość wycinka 10π tyle wiem, dalej mózg mi staje

Maslanek: Ten środek jest najgorszy. Bez niego to by było proste

Ada: brawo za spostrzegawczość xD

Maslanek: Beznadziejny ten środek... Nawet nie jestem w stanie wymyślić jak to zrobić w prosty sposób xd

Ada: to zrób w trudny jeśli masz jakiś pomysł to napisz, sama to oblicze

Maslanek: Jest wystarczająco trudny, że sam go nie zrobię

Eta:

	1
P≈329
	3

Maslanek: What way?

Eta:

	a2
P=		(3√3+2π −9)
	3

Jolanta:

	1		1
(		πr2−		20*20)*4
	4		2

Ada: można wiedzieć skąd ten wzór ?

Maslanek: Raczej nie . Wtedy masz dwa środki, Jolanta Zastanowię się w wolnej chwili nad tym wzorkiem Twoim Eta... Bo to cholernie interesujące

Jolanta:

	1		1
(		π*202−		*20*20)*4=400π−800
	4		2

Maslanek: 456,6370614359172953850573533118 Twój wynik wynosi tyle... Jak łatwo zauważyć to większe niż pole kwadratu...

Jolanta: Fakt trzeba jeszcze odjać środek

Eta:

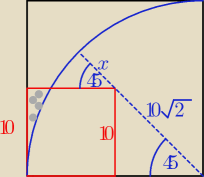
Artur z miasta Neptuna: Szukane pole = 20² − P_odpadu P_odpadu = 8*P_wyliczane P_wyliczane + P_{wycinek duży} = P_kwadrat + P_trójkąt + P_{wycinek mały}

	1		10*10		1
Pwyliczane +		π202 = 102 +		+		πx2
	8		2		8

	1
Pwyliczane + 50π = 100 + 50 +		π(20−10√2)2
	8

	1
Pwyliczane + 50π = 100 + 50 +		π(400−400√2 + 200)
	8

P_wyliczane + 50π = 100 + 50 + 75π −50√2π P_wyliczane = 150 + 25π − 50√2π ≈ 6.39567 P{odpadu} = 1200 + 200π − 400√2π ≈ 51.16536 Szukane P = 400√2π − 200π − 800 ≈ 348.83464 Ot takie ciekawe zadanko

Maslanek: Napisz, które to te pola . Bo wycinek duży, mały nic mi nie mówi

Eta:

Artur z miasta Neptuna: Dobra ... jest błąd ... bo P_{wycinek mały} nie jest wycinkiem okręgu o promieniu 'x'

Eta:

Artur z miasta Neptuna: wycinek duży −−− promień 20 wycinek mały ... to małe gówienko pomiędzy przerywanym promieniem a kwadratem

Artur z miasta Neptuna: ale można inaczej ... zrobię tylko rysunek ... a obliczenia jak wrócę z psem ze spaceru

Eta: Narysowałabym , ale nie umiem rysować łuków ( za Chiny mi nie wychodzą

Saizou : Eto, ostatni przycisk w pierwszym rzędzie, klikasz raz aby zahaczyć środek, a następnie mierzysz odległość, klikasz i rysujesz

Artur z miasta Neptuna:

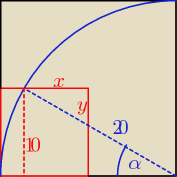
	10
(x+10)2 = 202 − 102 ... wyliczasz 'x' ... wyliczasz 'y' ... wyznaczasz α = 30o (		=
	20

sinα) I masz: P_kwadratu − P_{małego trójkąta w prawym rogu kwadratu} = P{wycinka koła o kącie 30^o) + P_{szukanego wypierdka} reszta jak wcześniej SZUKANE = 400 − wypierdek*8

Eta: Podaj pole "wypierdka"

Maslanek: Tamto było fajniejsze . Skąd to (x+10)²?

Artur z miasta Neptuna: x+10 −−− długość podstawy trójkąta ograniczonego dwoma przerywanymi (o dł 10 i 20)

Maslanek: Teraz już przejrzyste

Maslanek: Jutro spróbuję sam do tego dojść

Artur z miasta Neptuna:

10−y		√3		1		10(√3−1)		10(3−√3)
	= tg30o =		=		⇔ y =		=		=
10		3		√3		√3		3

	10√3
= 10 −
	3

x = ctg30^o*y = 10(√3 − 1)

	1
Pwypierdka = P□ + PΔ na prawo od kwadratu − Pmałego Δ −		400π =
	12

	10*(10−y)		x*y		100π
= 100 +		−		−		=
	2		2		3

	100√3		(10(√3 − 1))2√3		100π
= 100 +		−		−		=
	6		6		3

// 100(√3−1)²*√3 = 100(4√3 − 2*3) = 400√3 − 600 //

	100√3		100π
= 100 −		+ 100 −		≈ 8.6777
	2		3

P_szukane ≈ 330.5784

maniek: a ile Ci wyszło, bo mi ok 330,58

Ada/Daniel :D : ot ciekawostka prawda, dzięki za pomoc też robię to z czystej ciekawości

maniek: to się zgadza

Artur z miasta Neptuna: czyli Eta ... 'ździebko' więcej mi wyszło

maniek: w której klasie jesteście?

Artur z miasta Neptuna: maniek ... a do kogo było to pytanie ?

Eta:

400
	(5,2+6,28−9)= 133,3*2,48= 330,6
3

Eta: A jeszcze zapytam , bo jak długo żyję (a długo) to nie znam w matematyce pojęcia "wypierdek"

Artur z miasta Neptuna: Eta ... nie znasz figury 'wypierdek' ... no wiesz co ... wstydziłabyś się

Eta: ale nie znam

Ajtek: To wlasnie poznalas . Na jutro Artur... przygoruje Tobie jej wlasności . Cześć Artur... .

Mila: Pole trójkąta krzywoliniowego:( między listkami rozetki)

	1		a2√3
PΔ=a2−		Pkoła−
	6		4

Są 4 takie Δ.

	2
4*PΔ=4a2−		πr2−a2√3
	3

	2
Prozetki=a2−(4a2−		πr2−a2√3)=
	3

	2
=a2√3+		πa2−3a2
	3

Wynik liczbowy ....

Ajtek: Witaj Mila, no to mnie zabilas . Trójkąt krzywolinniowy, pierwszy raz o czyms takim slyszę .

Mila: Witaj Ajtek, no jakoś musiałam nazwać, a nie miałam ochoty rysować. Nie mów, że nie wiesz o czym mówię, moi uczniowie wiedzieli o czym mówię. W każdym bądź razie sposób jest krótki. Pozdrawiam.

Ajtek: Mila masz na mysli "to cos" zaznaczone na czetwono?

Mila: Jesteś wspaniały. Nie umiem tak rysować.O to właśnie mi chodziło. Nieustająco pozdrawiam. Dobranoc.

Ajtek: To ja Ciebie poucze rysować, a Ty mnie pouczysz matematyki, co Ty na to ? Spokojnej nocy . Będę jutro ok 21−szej, jak Rosjanie pojadą z treningu, a my sie jakoś szybko ogarniemy z murawą .

Mila: Dla Ciebie wszystko.

Ajtek: .

Artur_z_miasta_Neptuna: Mila ... a zdradź nam jeszcze − skąd ten wzór wyciągnęłaś − tylko nie mów że z jakiejś księgi (oczywiście mówię o polu 'wypierdka' vel trójkąta krzywoliniowego)

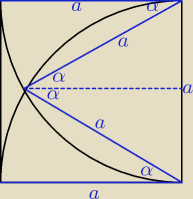
Basia: teraz już widać skąd Mila wzięła wzór

Mila: Basiu, zgadzam się co do joty. Tak właśnie ma być. Artur patrzyłam na rysunek Ady i co "widziałam", to przekładałam na wzory. Ciągle mam kłopoty ze zrobieniem rysunku. Pozdrawiam wszystkich.

Artur_z_miasta_Neptuna: mhm ... czyli po prostu troszeczkę szerzej spojrzałaś na problem niż ja

Eta: Wzór podany przez Milę taki sam,który podałam na samym początku

	a2		2
P=		(3√3+2π−9) = ..... = a2√3+		πa2−3a2
	3		3

Eta: @Maślanek I co doszedłeś do tego wzorku, który podałam, a Mila potwierdziła na nowo

Ada/Daniel :D : za nic w świecie nie wiem skąd ten wzór, patrze analizuje i nie pojmuję

Artur_z_miasta_Neptuna: Trójkąt mający boki − prawy bok kwadratu, promienie zbiegające do przecięcia się dwóch łuków ... jest trójkątem równobocznym (boki równe promieniowi) ... stąd α = 30^o. Skoro α = 30^o to dolny wycinek koła (poniżej trójkąta) = + to w takim razie górny wycinek koła (powyżej trójkąta) = + pole trójkącika równobocznego = Teraz pole kwadratu − to co wyliczyłeś/−aś przed chwilą.

Mila: Ada − dwa wycinki koła o kącie środkowym 30⁰ =jeden wycinek o kącie środkowym 60 ⁰ a to jest 1/6 koła. Obróć rysunek Basi o 90⁰ to zobaczysz.

Ada/Daniel :D : właśnie ta 1/6koła mnie wybijała z rytmu dzięki wielkie, czuje się mądrzejszy

MQ: Sądząc po rysunku Ajtka z 00:40 (oczywiście obróconym o 90^o, to "wypierdkiem" nalezałoby raczej nazwać właśnie to, co Mila −− elegancko −− nazwała "trójkątem krzywoliniowym" . Swoją drogą, piękne zadanie i eleganckie rozwiazania .

Ada/Daniel :D : chcecie więcej ?

Artur_z_miasta_Neptuna: a dawaj ... przynajmniej był jakiś przykład, którego się nie robiło 'od ręki'

Mila: Artur, jest tam całka do zrobienia, ja mam długi sposób.

Artur z miasta Neptuna: gdzie gdzie gdzie <ślini się>

Maslanek: Nie miałem czasu się skupić Zapomniałem całkiem o problemie