nierówności kwadratowe
PIOTR: Rozwiąz nierówności
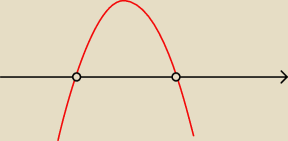
−2x2−x+3<0
3 cze 15:41
alexandra:
−2x
2 − x + 3 < 0
a = −2
b = −1
c = 3
Δ = b
2 − 4ac = (−1)
2 − 4 * (−2) * 3 = 1 + 24 = 25
√Δ =
√25 = 5
| | −b−√Δ | | −(−1)−5 | | 1−5 | | −4 | |
x1 = |
| = |
| = |
| = |
| = −1 |
| | 2a | | 2*(−2) | | −4 | | −4 | |
| | −b+√Δ | | −(−1)+5 | | 1+5 | | 6 | | 3 | | 1 | |
x2 = |
| = |
| = |
| = |
| = − |
| = −1 |
| |
| | 2a | | 2*(−2) | | −4 | | −4 | | 2 | | 2 | |
| | 1 | |
x∊ (−∞, −1 |
| ) ∪ (−1,+∞) |
| | 2 | |
3 cze 22:27
pigor: ... lub tak :
−2x2−x+3<0 /:(−2) ⇔ 2x
2−2+x−1>0 ⇔ 2(x−1)(x+1)+1(x−1)>0 ⇔
⇔ (x−1)(2x+3)>0 ⇔ 2(x−1)(x+
32)>0 ⇔
x<−32 lub
x>1 , czyli
x∊(−∞;−32) U (1;+∞) . ...
3 cze 22:44
ManFanUtd: Błąd w x1 minus : minus = plus czyli U{−4}{−4|=1
3 cze 22:45