licze na Waszą pomoc nadia: proszę pomóżcie, bo męczę się strasznie z tym zadaniem i nie daje mi ono spokoju: udowodnij tożsamość trygonometryczną ^{ctgx − tgx}_{sinx + cosx} = ¹_sinx − ¹_cosx

nadia:

nadia: proszę pomóżcie

Eta: Licznik

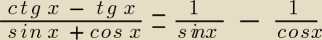
cosx		sinx		cos2x−sin2x		cosx−sinx)(sinx+cosx)
	−		=		=
sinx		cosx		sinx*cosx		sinx*cosx

M=(sinx+cosx)

L		cosx−sinx		cosx		sinx		1		1
	=		=		−		=		−
M		sinx*cosx		sinx*cosx		sinx*cosx		sinx		cosx

Mila: zał. sinx≠0 i cosx≠0

	cosx		sinx
L=(		−		):(sinx+cosx)=
	sinx		cosx

	cos2x−sin2x
=		:(sinx+cosx)=
	sinx*cosx

	(cosx−sinx)*(cosx+sinx)		1
=		*		=
	sinx*cosx		(sinx+cosx)

	(cosx−sinx)		cosx		sinx
=		=		−		=
	sinx*cosx		sinx*cosx		sinx*cosx

	1		1
=		−		=P
	sinx		cosx

nadia: dziękuję bardzo!

pigor: ... np. tak :

	ctgx−tgx		cosx   sinx   − sinx   cosx
L=		=		=
	sinx+cosx		sinx+cosx

	cos2x−sin2x		(cosx−sinx)(cosx+sinx)
=		=		=
	sinx cosx (sinx+cosx)		sinx cosx (sinx+cosx)

	cosx−sinx		1		1
=		=		−		= P . ...
	sinx cosx		sinx		cosx

nadia: nie wpadłam na to: cos²x−sin²x −−−> (cosx−sinx)(sinx+cosx) −.−