geometria analityczna Moniśka: Proszę o pomoc w zadaniu: Wyznacz punkt symetryczny do A względem l jeśli: A= (1,8) l: −x − 2y + 2= 0

daveustro: A' = (−5, −4)

Moniśka: mogę zapytać skąd to się wzięło?

anies: najpierw musisz wyznaczyć prostą prostopadłą do l a₂=−¹_a1 przekształcasz wzór prostej l y=−¹₂x+1 więc prosta prostopadła to y=−2x+1 prosta ta musi przechodzić przez punkt A= (1,8) podstawiamy do wzoru prostej 8=−2*1+b b=10 równanie prostej prostopadłej przechodzącej przez punkt A to y=−2+10 teraz znajdujemy punkt wspólny dla obu prostych y=−2+10 y=−¹₂x+1 czyli innymi słowy robisz równanie

anies: oczywiście ma być y=−2x+10 bo mi się zjadło

anies: x=6 y=−2

anies: teraz obliczasz tylko odległość punktów A= (1,8) i x=6 y=−2 mnożysz i masz

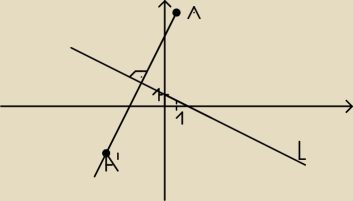
daveustro: −x − 2y + 2 = 0 y = −x/2 + 1

daveustro: a nie można takich rzeczy wnioskować z rysunq? po kratkach na przykład... przy dobrym rysunq wszystko widać. właśnie z tym mam problem, że za dużo upraszczam i pewnie na maturze straciłbym za to pkty, co?

anies: prawdziwy matematyk życie sobie upraszcza ale na maturze masz się wstrzlić w klucz, a profesorowie na uczelni każą wszystko tłumaczyć... wtedy matma nie jest królową nauk

♊: daveustro − a jak odróżnisz punkt (−5,0000000000000000000001 ;−4) od (−5 ;−4) ? Na arkuszu maturalnym masz kratki wystarczające by nanieść odpowiednio dokładne oznaczenia? Jeżeli w poleceniu nie pisze rozwiąż graficznie to nie odczytujesz z rysunku.

daveustro: tego się właśnie obawiałem... zrobiłem sobie właśnie próbną z dzisiejszej wyborczej i połowę zadań za 6, 5 pktów porobiłem w dwóch linijkach i rysunq... a najgorsze jest to, że nie pamiętam, jak się to robiło lekcyjnie krokami... tydzień czasu mi został, żeby sobie przypomnieć o.O

Moniśka: dziękuję za pomoc

daveustro: ale II nie mów, bo idzie zauważyć zależność... jak idzie Ci prosta wektorem [2,−1] to prostopadła będzie musiała iść [1,2]. jeżeli pkt A ma dokładnie (1,8), to nie będzie żadnych ,0000000001... to nie ten poziom matematyki... w gimnazjum, czy tam liceum zadania geometryczne nie operują takimi liczbami... przecież