ZADANIE FRYTA: Punkty A = ( 1, 5 ), B = ( 14, 31 ) , C = ( 4, 31 ) są wierzchołkami trójkąta. Prosta zawierająca wysokośd tego trójkąta poprowadzona z wierzchołka C przecina prostą AB w punkcie D. Oblicz długośd odcinka BD.

Bezimienny: 1) rownanie prostej przechodzacej przez punkty A i B 2) a₁ * a₂ = −1 3) rowanie prostej przechodzacej przez punkt C i a₂ wyliczone z punktu 2) 4) punkt wspolny D dwoch prostych:1) i 3) 5) dlugosc wektora BD

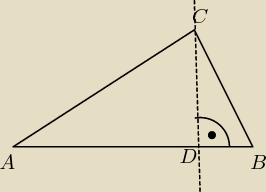
Gustlik: Dane: A = ( 1, 5 ), B = ( 14, 31 ) , C = ( 4, 31 ) Obliczam z wektorów współczynnik kierunkowy prostej AB: AB^→=[14−1, 31−5]=[13, 26]

	26
aAB=		=2
	13

	1
aCD=−		(z war. prostopadłości prostych)
	2

Wysokość CD ma równanie:

	1
y=−		x+b
	2

	1
31=−		*4+b
	2

31=−2+b 33=b b=33

	1
y=−		x+33
	2

Przekształcam na równanie ogólne:

	1
0=−		x−y+33 /*(−2)
	2

x+2y−66=0

	|Ax0+By0+C|
Korzystam ze wzoru na odległość punktu od prostej: d=		,
	√A2+B2

B = ( 14, 31 ), odcinek BD to odległość punktu B od wysokości CD:

	|14+2*31−66|		|10|		10√5
|BD|=		=		=		=2√5
	√12+22		√5		5