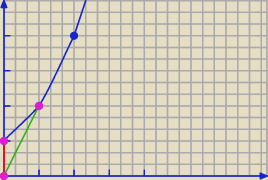
pole obszaru student: Witam, mam problem z jednym zadaniem. 1.Oblicz pola obszarów ograniczonych krzywymi y=2^x, y=2x, x=0. Wykres narysowałem, ale nadal jakoś mało mi to mówi i nie wiem co dalej z tym . Będę wdzięczny za rozwiązanie tego zadania!

Godzio: ∫⁰₁(2^x − 2x)dx

student: Czyli byłem bliski rozwiązania dzięki Godziu !

Godzio: ∫₀¹ oczywiście (źle granice napisałem )

student: A jeszcze takie pytanie. Bo nie do końca rozumiem, które proste wybrać do tej całki.. Rozumiem, że te, które się przecinają, a co z 2^x i x=0, one też się przecinają. Tak samo 2x i x=0. Czy prostu ze względu na to, że jest to 0 to nie bierzemy prostej x=0 pod uwagę?

Basia: prosta x=0 to oś OY; oczywiście, że bierzemy ją pod uwagę; gdyby jej nie było obszar byłby nieograniczony

Godzio: Jak nie bierzemy ? Prosta x = 0 ogranicza nam lewą stronę, bierzemy tę część, o którą nas proszą w poleceniu "obszar ograniczony y = 2^x, y = 2x, x = 0 ". Czyli to czego szukamy musi się zawierać między tymi trzeba krzywymi, nie możemy wziąć np. obszaru ograniczonego 2^x i 2x bo jakby dalej pociągnąć wykresy to one się znów przetną w punkcie (2,4)

student: Fakt, oczywiście racja. Tylko jeszcze chodzi mi o jedną rzecz. Dajmy na to to zadanie. Mamy te 3 proste, rysujemy wykres, widzimy gdzie się przecinają. To na podstawie czego mamy wiedzieć z których skonstruować całkę do obliczenia pola obszaru ? ( zadaje może banalne pytania, ale nie do końca to rozumiem )

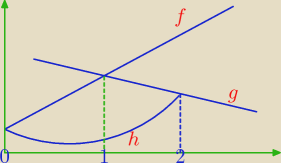
Godzio: Masz tu taki typowy przykład, gdzie trzeba napisać 2 całki, widać, że na przedziale [1,2] funkcja f nie ma nic do gadania, a wyższą funkcją staje się g, więc pole obszaru wyrazi się tutaj: ∫₀¹(f − h)dx + ∫₁²(g − h)dx Nie wiem czy to takie oczywiste, trzeba porobić parę przykładów, żeby to lepiej zrozumieć

student: Ok, dzięki, poćwiczę jeszcze i mam nadzieje, że ogarnę .