Analiza matematyczna student: KOL1 http://www.sendspace.pl/file/3378a36df92d104a71dcb22 KOL2 http://www.sendspace.pl/file/f3d52bab41e5acb8c5384f7 KOL3 http://www.sendspace.pl/file/c9ea7e1676d7a8db8307561 Prosiłbym o pomoc w zadaniach 1,5,6 w każdej z tych list zadań

Godzio: Jeśli nikt nie pomoże, to odśwież ten post koło 20 to Ci pomogę (bez zad. 4 bo jeszcze tego nie przerabiałem)

student: tylko 1;5;6 zad 4 nie trzeba

Godzio: No chodziło mi o 6 Bo całek podwójnych jeszcze nie miałem

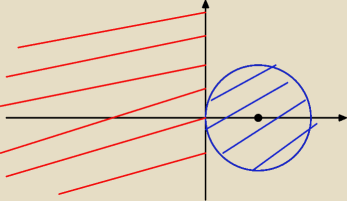
Basia: x²+y² ≤2y x² + y² − 2y ≤ 0 x² + (y − 1)² − 1 ≤ 0 x² + (y−1)² ≤ 1 koło: S(0,1) r = 1 x≤0 półpłaszczyzna od OY w lewo coś tu jest źle bo te obszary mają jeden punkt wspólny O(0,0) czyli byłaby ₀∫⁰ dx ₀∫⁰ y dy = 0 ale to jest bez sensu może tak miało być y≤0 albo np. x≤1 wtedy to miałoby jakiś sens

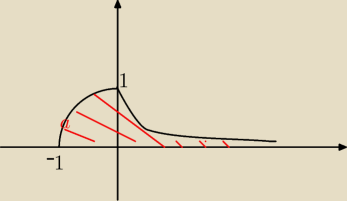
Basia: zadanie 1; lista 1 P = ₋₁∫⁰ (1−x²)dx + ₀∫^+∞ 2^−x dx = [ x − ¹₃x³ ]₋₁⁰ + lim_{a→+∞ 0}∫^a 2^−x dx = [ 0 − ¹₃*0³ − ( −1 − ¹₃*(−1)³ ) ] + lim_a→+∞ [ U{2^−x}{ln2 ]₀ ^a =

	2−a		2−0
[ 1 + 13*(−1) ] + lima→+∞ [		−		] =
	ln2		ln2

	1		1
U{2}[3} +		lima→+∞ [		− 1 ] =
	ln2		2a

2		1		2		1
	+		*[ 0 −1 ] =		−
3		ln2		3		ln2

Basia: zadanie 5; lista 1 g(x,y) = x³ + 8y³ −6xy + 5 g'_x = 3x² − 6y g'_y = 24y² − 6x 3x² − 6y = 0 /:3 24y² − 6x = 0 /:6 x² − 2y = 0 4y² − x = 0 2y = x² (2y)² − x = 0 (x²)² − x = 0 x⁴ − x = 0 x(x³ − 1) = 0 x(x−1)(x²+x+1) = 0 x = 0 lub x=1 (równanie x²+x+1=0 nie ma rozwiązania) możliwe punkty stacjonarne to A(0[0) i P(1; ¹₂) g"_xx = 6x g"_xy = −6 g"_yx = −6 g"_yy = 48y hesjan W(x,y) = 6x*48y − (−6)*(−6) = 288xy − 36 W(1; ¹₂) = 288*1*¹₂ − 36 = 144 − 36 = 108 > 0 czyli w punkcie P ekstremum istnieje W(0,0) = 288*0*0 − 36 = −36 < 0 czyli w punkcie A ekstremum nie istnieje ale Ty masz zbadać P g"_xx(1;¹₂) = 6*1 = 6 > 0 czyli w p−cie P(1;¹₂) mamy minimum lokalne

Basia: zadania z pozostałych list są bardzo podobne; próbuj sam i pytaj jeżeli będą problemy

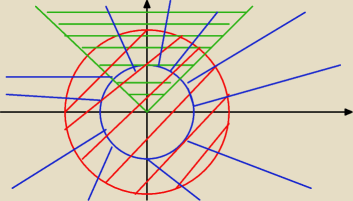
Basia: zadanie 6; lista 2 x²+y² ≤ π^ koło S(0,0) r=π (kolor czerwony)

	π2
x2+y2 ≥
	4

okrąg S(0,0) i t=^π₂ i jego zewnętrze (niebieski) y ≥ |x| (zielony) P= _{√(π²/4)−x²}∫^√π2−x2dx ∫_−π∫^−π₂ cos√x²+y²dy + _{√(π²/4)−x²}∫^√π2−x2dx ∫_^π2∫^π cos√x²+y²dy ale ja bym tu raczej zastosowała współrzędne biegunowe r ∊ <−π;−^π₂> ∪ <^π₂; π> φ ∊ <^π₄; ^3π₄> x = r*cosφ y = r*sinφ cos√x²+y² = cosp{r²cos²φ + r²sin²φ) = cosp{r²(sin²φ+cos²φ) = cos√r² = r P = _^π2∫^3π₄ dφ _−π∫^π₂ r dr + _^π4∫^π₂ dφ _^π2∫^π r dr

student: Dzięki, ale mogłabyś wyjaśnić skąd wziełaś r i φ