Geometria
Alfa: Mam do rozwiązania zadania z geometrii :
Pole prostokąta, w którym jeden z boków jest 3 razy dłuższy od drugiego, wynosi 48 cm2. Oblicz
kąt między prostokątnymi.
Boki wyszły mi : a=4 i b=12, a co z tymi kątami, proszę pomóżcie.
i jakby ktoś miał czas to mam jeszcze jedno zadanie, dłuższe, strasznie dziwne rzeczy mi
wychodzą:
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 4cm, Spodek tej
wysokości leży w odległości 116 cm od środka okręgu opisanego na tym trójkącie. Oblicz:
a)długość promienia okręgu opisanego na tym trójkącie
b)długość boków tego trójkąta
2 cze 11:35
Alfa: sory w pierwszym zadaniu : oblicz kąt między przekątnymi prostokąta
2 cze 11:37
Basia:
ad.1
oblicz teraz długość przekątnej d (w prostokącie są one równe i przecinają się w połowie
narysuj je
widzisz 4 trójkąty; wybierz sobie jeden np. ten o bokach d2, 3, d2
i zastosuj tw.cosinusów
2 cze 11:43
Maslanek: Oblicz długość przekątnej i skorzystaj ze wzoru na pole czworokąta:
gdzie γ to kąt między przekątnymi.
2 cze 11:45
Alfa: cóż nie miałam na podstawie tw. cosinusów ale spróbuję
2 cze 11:48
Basia:
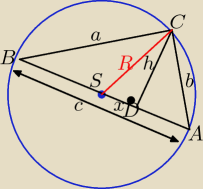
h = 4
x = 1
16 =
76
R policz z tw. Pitagorasa w tr.SDC
c = 2R
BD = R+x i tw.Pitagorasa w tr. BDC
AD = R−x i tw.Pitagorasa w tr. ADC
2 cze 11:51
Skipper:
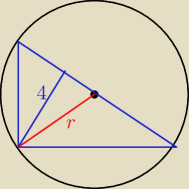
r
2=16+(7/6)
2=16+49/36=625/36
r=25/6
...dalej chyba już jasne−
2 cze 11:55
Alfa: wielkie dzięki wam wszystkim
2 cze 12:04
Basia:
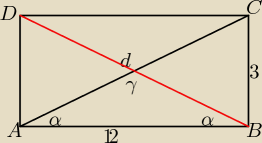
bez tw.cosinusów
tr.ABC jest prostokątny
d
2 = 3
3+12
2 = 9+144 = 153 = 3*51 = 3*3*17
d = 3
√17
niedokładnie:
| | 3 | | 1 | |
sinα = |
| = |
| ≈ ..... |
| | 3√17 | | √17 | |
z tablic odczytujesz α
γ = 180 − 2α
dokładnie:
| | 1 | | 4 | | 8 | |
sinγ = sin(180−2α) = sin2α = 2sinα*cosα = 2* |
| * |
| = |
| |
| | √17 | | √17 | | 17 | |
| | 16 | | 1 | | 15 | |
cosγ = cos(180−2α) = −cos2α = −cos2α+sin2α = − |
| + |
| = − |
| |
| | 17 | | 17 | | 17 | |
albo z tw.sinusów
| | sinα | | | | 12*2 | | 8 | |
sinγ= 12*2* |
| = 12*2* |
| = |
| = |
| |
| | d | | 3√17 | | 3*17 | | 17 | |
2 cze 12:06