geometria m: Wykaż że jeżeli jeden z kątów trójkąta jest równy π/6 to długość boku przeciwległego temu kątowi jest równa promieniowi okręgu opisanego na tym trójkącie.

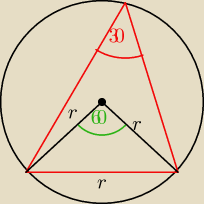
Artur z miasta Neptuna: Z tw. o kątach opartych na tym samym łuku, wiesz że zielony kąt ma miarę ^π/₃ (czyli 60^o). czarne boki dolnego trójkąta mają miarę 'r'. Masz więc do czynienia z trójkątem równoramiennym,

	180 − 60
a więc kąty u podstawy są równe i wynoszą		= 60o.
	2

Czyli jest to trójkąt równoboczny ... a więc podstawa = r. c.n.w.

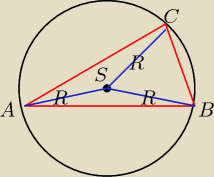
Basia: ∡BAS = ^π₆ = 30^o to jaka jest miara ∡BSC ? i jakim trójkątem jest wobec tego tr.BSC ? i co z tego wynika ?

kylo1303: Mozna tez skorzystac z tw. sinusow, nie trzeba wtedy nic rysowac.

Eta: Dokładnie