geometria m: Z dwóch przeciwległych wierzchołków kwadratu zakreślono okręgi o promieniu równym długości boku tego kwadratu. Pole figury ograniczonej łukami tych okręgów i zawartej w kwadracie wynosi (2π − 4)cm². Jaka jest długość boku tego kwadratu?

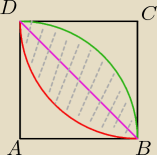
Artur z miasta Neptuna: dolna część zakreskowanego pola (od czerwonego łuku do filetowej przekątnej) wyliczam następująco:

	1		1
Px = Pwycinek okręgu o promieniu a − PΔBCD =		πa2 −		a2
	4		2

	1
Polec zakreskowanego pola = 2*Px =		πa2 − a2
	2

a stąd wynika, że a² = 4 ⇒ a=2

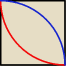
Maslanek: Te skrawki kwadratu mają pole:

	πr2		4a2−πa2		πa2
Ps = 2*P1 = 2*(a2−		) = 2*		= 2a2−		.
	4		4		2

Czyli pole między tymi łukami, to:

	πa2		πa2−2a2
Px = Pkw − Ps = a2 − 2a2+		=		.
	2		2

Skoro P_x= 2π−4, to a=2 cm.