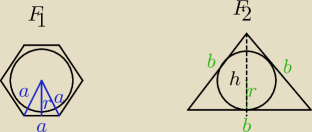geometria m: wykaż że pole 6kąta foremnego opisanego na pewnym okręgu stanowi 2/3 pola trójkąta równobocznego opisanego na tym okręgu

Beti: sześciokąt: P_F1 = 6P_t

	a√3		2r
r =		−−> a =
	2		√3

	a2√3		4r2   √3 3		r2√3
Pt =		=		=
	4		4		3

	r2√3
PF1 = 6*		= 2√3r2
	3

trójkąt:

	b2√3
PF2 =
	4

	1		1	b√3		6r
r =		h =			−−> b =		= 2√3r
	3		3	2		√3

	12r2√3
PF2 =		= 3√3r2
	4

	2		PF1		2
TEZA: PF1 =		PF2 −−>		=
	3		PF2		3

	PF1		2√3r2		2
D−D:		=		=
	PF2		3√3r2		3

cbdw

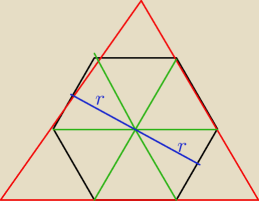+-: Jak widac na rysunku trójkąt równoramienny liczy dziewięć mniejszych, a sześciokąt foremny sześć czyli 6/9 =2/3