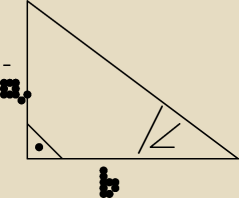
Zadanie Kaśka: Dany jest trójkąt prostokątny, w którym a,b oznaczają długości przyprostokątnych , α jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej α, Wiadomo,że sinα √10 / 10. Oblicz: a) tangens kąta α

	a		b2
b) wartość wyrażenia: 3*		+ 2*
	a−b		a2+b2

Klara: Pomagam

Klara: wiesz napewno ,że tgα= ^sinα_cosα mając sinα= ^√10₁₀ oblicz cos²α z jedynki tryg. i po podstawieniu do tgα obliczysz tgα powinien wyjsć : tgα= ¹₃ b) juz prosto : ponieważ tgα= ^a_b więc ^a_b = ¹₃ => b = 3a podstaw do tego wyrazenia za b= 3a i oblicz te wartość powinna Ci wyjść ³₁₀ dasz radę , powodzenia