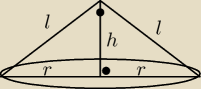
tworzaca maciej: przekroj osiowy stozka jest trojkatem prostokatnym. objetosc stozka jest rowna ⁸₃pi . Oblicz dlugosc tworzacej l

Beti: przekrój osiowy jest trójkątem prostok., więc z tw. Pitagorasa l²+l²=(2r)² 2l² = 4r²

	1
r2 =		l2
	2

	√2
r =		l
	2

z trójkata prostok. o bokach h,r,l mamy: h² + r² = l²

	1
h2 +		l2 = l2
	2

	1
h2 =		l2
	2

	√2
h =		l
	2

dana jest objętość stożka, więc:

	1		8		3
V =		πr2h =		π /*
	3		3		π

r²h = 8

	1		√2
		l2*		l = 8 −−> po podstawieniu
	2		2

	√2
		l3 = 8 /*4
	4

√2l³ = 32 /:√2

	32
l3 =		= 16√2 = 24*21/2 = 29/2
	√2

l = (2^9/2)^1/3 = 2^3/2 = √2³ = √8 = 2√2