geometria analityczna mixek: 1. wyznacz zbiór wszystkich środków cięciw okręgu o równaniu x²+y²−4x=0 przechodzacych przez punkt A=(0,0) 2. punkt a=(2,5) jest środkiem cięciwy paraboli o równaniu y²=20x . Napisz równanie prostej zawierającej tę cięciwe. Bardzo proszę o pomoc.

mixek: pomoze mi ktoś?

Basia: jeżeli nikt inny się nie zgłosi, to mogę pomóc mniej więcej za godzinę (teraz muszę przerwać) jakby co to podbij tak koło 21:20

mixek: okey dzięki, będę czekał

karla: Też będę wdzięczna za rozwiązanie zadania w 2 wyszło mi y=4x−22 nie wiem czy jest dobrze

mixek: karla w moim zbiorze wynik tego 2 to y=2x+1

mixek: i jak Basia pomozesz?

Basia: ad.1 x∊<−4; 0> B∊ okręgu ⇒ B(x; √4x−x²) lub B(x; −√4x−x²) ⇒

	x
S(		; U{√4x−x2{2}} lub S(x; −U{√4x−x2{2}}
	2

czyli t = ^x_t t∊<−2;0> x = 2t

	√4*2t − 4t2		2√2t − t2
y =		=		= √2t−t2
	2		2

lub

	√4*2t − 4t2		2√2t − t2
y = −		= −		= −√2t−t2
	2		2

czyli zbiór środków cięciw = { (x,y): x∊<−2;0> ∧ [ y = √2x−x² lub y= −√2x−x² ] }

mixek: najmocniej przepraszam cię,ale nic z tego nie rozumiem... co to jest za pkt B? dlaczego x∊<−4,0>?

mixek: a rozwiąże ktoś może 2 zadanie?

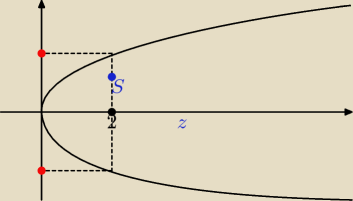
Basia: widać od razu, że prosta x=2 odpada y = ax+b 5 = a*2+b b = 5−2a y = ax+5−2a szukamy punktów wspólnych prostej i paraboli (ax+b)² = 20x a²x² + 2abx + b² − 20x =0 a²x² + x[ 2a(5−2a) − 20] + (5−2a)² = 0 a²x² + (−4a²+10a−20)x + (5−2a)² = 0

x1+x2
	= 2
2

x₁+x₂ = 4 z wzorów Viete'a

	4a2−10a+20
x1+x2 =
	a2

4a2−10a+20
	= 4
a2

4a² − 10a + 20 = 4a² −10a+20 = 0 /:(−10) a − 2 = 0 a=2 b = 5 − 2*2 = 1 czyli prosta ma równanie: y = 2x+1

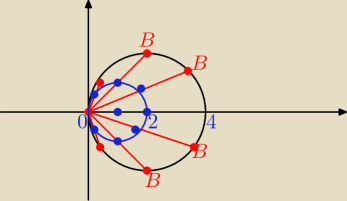
Basia: rysunek do zadania 1 to są możliwe położenia drugich końców cięciw (oczywiście nie wszystkich) środki tych cięciw układają się w ten niebieski okrąg nie dopisałam tam ostatniego wiersza czyli zbiór środków cięciw = { (x,y): x∊<−2;0> ∧ [ y = √2x−x² lub y= −√2x−x² ] } = { (x,y): x∊<−2;0> ∧ y² = 2x −x²} = { (x,y): x∊<−2;0> ∧ x²+y²−2x = 0 } czyli jest to okrąg S₁(1;0) i promieniu r₁ = 1 −−−−−−−−−−−−−−−−−−− co do Twojego pytania o dziedzinę tam się oczywiście pomyliłam x∊<0;4> t∊<0;2>

mixek: mam jeszcze jedno zadanie treść taka sama jak w 1 ale okrąg ma równanie x²+y²−2x−3y=0 a pkt A=(0,0). Wiem, że jest to ten sam sposób jak twój, ale już pojawaiają się kłopoty przy liczeniu. Pomozesz mi? Będę ci bardzo wdzięczny.

Basia: no bo tu niestety będzie trudniej, ale da się zrobić; za kilka minut się tym zajmę, a pisanie też trochę potrwa a poprzednie oba zrozumiałeś ?

Basia: jesteś pewny, tych danych ? to jest rachunkowo koszmarne

mixek: tak to ze zbioru i ty zostaniesz euklidesem, treść jest w porządku. Tak poprzednie zrozumiałem

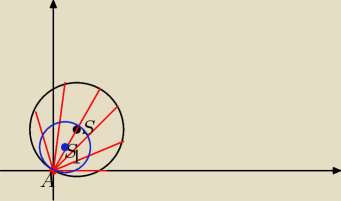
Basia: przez analogię można się domyślić

	√13
mamy S(1; 32) i r =		)
	2

to środek tego nowego S₁ będzie środkiem odcinka AS czyli S₁ (¹₂; ³₄)

	r		√13
a promień r1 =		=
	2		4

czyli równanie (x − ¹₂)² + (y−³₄)² = ¹³₁₆ x² − x + ¹₄ + y² − ³₂y + ⁹₁₆ = ¹³₁₆ x² +y² − x − ³₂y =0 ale policzenie tego tak elegancko jak zostało policzone poprzednie jest niemal niemożliwe niewykluczone, że trzeba jakąś sztuczkę zastosować, ale nie wiem czy tak zaraz uda mi się na nią wpaść

mixek: wielkie dzięki. to na dzisiaj wystarczy. Jak ja się tobie odwdzięczę...? Jeszcze raz bardzo mocno Ci dziękuję.

Basia: zostań znakomitym matematykiem

Basia: sztuczka powinna chyba polegać na przesunięciu okręgu początkowego o wektor u^→[−1; −³₂] dostaniemy wtedy okrąg x²+y² = ¹³₄ A(−1; − ³₂) liczymy tak jak w pierwszym zadaniu i przesuwamy "z powrotem" czyli o wektor −u^→[1; ³₂]

mixek: dowiedziałem się od mojego nauczyciela,że należy napisać równanie prostej przez punkt A=(0,0). czyli y=mx, po czym stworzyć układ równań z tą prostą oraz równaniem okręgu. potem delta, współrzędne punktów B i C, układ równań parametrycznych i z tego układu wyjdzie nowa krzywa, która w obu przypadkach jest okręgiem bez punktu A=(0,0). Jeszcze raz bardzo dziękuję. Pozdrawiam.

mixek: a pomiędzy pkt B i c a układem parametrycznym należy jeszcze obliczyć srodek odcinka B i C.

Mila: Tak właśnie mam zrobione, ale to zadanie to szczególny przypadek, bo Ta prosta przechodzi przez punkt (0,0) i okręgi też, jedno rozwiązanie już jest. Rozwiązanie Basi jest bardzo dobre. Jeśli nie masz zrobionego z parametrem to mogę napisać. Pan podał wam ogólną zasadę.

mixek: zadanie zrobiłem, ale nie wychodzi mi z okręgiem o równaniu x2+y2−2x−3y=0 a pkt A=(0,0).

Mila: Jakie masz równanie w przypadku:x²+y²−4x=0 x_s=.. y_s=..? Co Ci w drugim okręgu nie wychodzi?

mixek: już za deltą gdzieś mam jakąś pomyłkę

mixek: wychodzi ze x=0 i y= 0 lub x=⁴_1+m² i y+^4m_1+m² czyli to sa dwa pkt B i C. środek tego odcinka BC jest pkt S, gdzie x=²_1+m² i y=^2m_1+m² i to jest ten układ równań parametryczny. i z niego wychodzi że nowy okrąg ma rówanie (x−1)²+y²=1 i A nie nalezy do tego okręgu, co jest zgodne z odpowiedzią.

mixek: to jest oczywiście do pierwszego równania.

Mila: Tak samo mi wyszło. Ale Basia ma takie samo równanie. W drugim okręgu mam:

	3m+2
x=
	m2+1

	3m+2
y=m*
	m2+1

Mila: Za wczesnie wysłałam:B=(0,0) To współrzędne drugiego punktu na okręgu C=(.,.) wysłałam.

Basia: to bardzo dobry sposób z tą prostą zwracam tylko uwagę, że w drugim przykładzie nie każda prosta zawierająca cięciwę ma równanie y = mx jest jedna, która ma równanie x=0 [ cięciwa AB gdzie A(0,0) B(0,3) ] i należy to uwzględnić, bo w równaniu parametrycznym zabraknie punktu P(0,³₂)