geometria marta: W kole o srodku O poprowadzono dwie prostopadle srednice AB i CD oraz cieciwe AM przecinającą srednice CD w punkcie K. Oblicz miare kata BAM wiedzac, ze w czworokat OBMK mozna wpisac okrag.

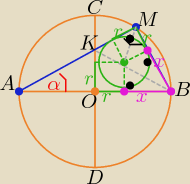
Eta: Trójkąt ABM jest prostokątny , bo kąt AMB jest kątem wpisanym opartym na średnicy AB Okrąg wpisany w czworokąt OBMK jest również wpisany w trójkąt ABM zatem: |OB|= x+r i |BM|=x+r ⇒ |OB|= |BM| to: |AB|=2|BM|

	|BM|		|BM|		1
sinα=		=		=
	|AB|		2|BM|		2

to α= 30^o