Pilnie potrzebuje pomocy :) twierdzenie cosinusow Krzysiek :D: W trójkącie ABC długość boku b=4, a boku c=6. Miara kąta leżącego naprzeciwko boku a jest dwa razy większa niż miara kąta leżącego naprzeciwko boku b. oblicz długość boku a.

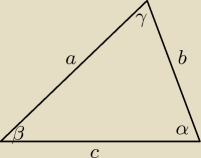
Basia: α=2β α=2β< 180 ⇒ β<90 a² = b²+c²−2bc*cosα = 16+36−2*4*6*cos(2β) = 52−48cos(2β)

sinα		sinβ
	=
a		b

a*sinβ = b*sinα

	b*sin(2β)		b*2sinβ*cosβ
a =		=		= 2b*cosβ= 8cosβ
	sinβ		sinβ

64cos²β = 52 − 48cos(2β) /:4 16cos²β = 13 − 12*(2cos²β−1) 16cos²β + 24cos²β =13 40cos²β = 13

	13
cos2β =
	40

	√13
cosβ = U{√13{√40} =
	2√10

	√13		4√130		2√130
a = 8*		=		=
	2√10		10		5

Krzysiek :D: Wynik w ksiazce wychodzi niestety 2√10

Eta: Szkoda,że nie zauważyłeś zwykłego przeoczenia przez Basię 16cos²β=13−12(2cos²β−1) i teraz powinno być: 16cos²β+24cos²β= 25

	25		√10
co daje : cos2β=		⇒ cosβ=
	40		4

	√10
a= 8cosβ= 8*		= 2√10
	4

i jest ok

Basia: sprawdź; może się gdzieś w rachunkach pomyliłam i nawet wiem gdzie szósty wiersz od dołu 16cos²β = 13 − 12*(2cos²β−1) to jeszcze dobrze potem powinno być 16cos²β = 13 − 24cos²β+12 40cos²β = 25

	25		5
cos2β =		=
	40		8

	√5		√40		2√10		√10
cosβ =		=		=		=
	√8		8		8		4

	√10
a = 8*		= 2√10
	4

Basia: Witaj Eto ! wniosek: nawet rachunków nie chciało się przeczytać; wynik z książki i koniec Krzysiek: D tak się nie nauczysz matematyki

Eta: Witaj Basiu