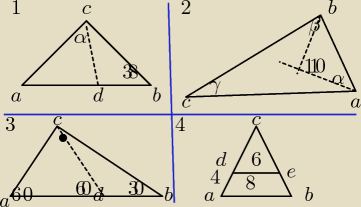
 1. Trójkąt ABC i BCD są równoramienne , w czym IACI=IBCI i IDCI=IDBI. Wynika z tego , że miara
kąta α jest równa;
a)38 stopni b)66stopni c)71stopni d)76stopni
2. Kąt miedzy dwusiecznymi kątów α i β , ma miare 110 stopni. Kąt γ w tym trójkącie ma miarę:
a)30 stopni b)40 stopni c)45 stopni d)70 stopni
3. Długość odcinka DB wiedząc że odcinek IacI = √2 w trójkącie ABC jest równa?
4.Odcinek DE jest równoległy do podstawy trójkąta ABC . Długość odcinka DC jest równa:
a)14 b)12 c)9 d)3
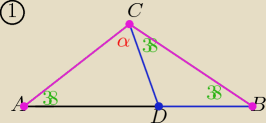
1. Trójkąt ABC i BCD są równoramienne , w czym IACI=IBCI i IDCI=IDBI. Wynika z tego , że miara
kąta α jest równa;
a)38 stopni b)66stopni c)71stopni d)76stopni
2. Kąt miedzy dwusiecznymi kątów α i β , ma miare 110 stopni. Kąt γ w tym trójkącie ma miarę:
a)30 stopni b)40 stopni c)45 stopni d)70 stopni
3. Długość odcinka DB wiedząc że odcinek IacI = √2 w trójkącie ABC jest równa?
4.Odcinek DE jest równoległy do podstawy trójkąta ABC . Długość odcinka DC jest równa:
a)14 b)12 c)9 d)3
 :(
:(
 1/
38+38+38+α=180 ⇒ α=...
1/
38+38+38+α=180 ⇒ α=...
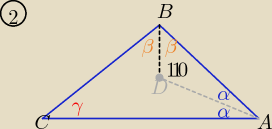 Z ΔADB α+β= 70o
to w ΔABC 2α+2β= 140o ⇒ γ = 180o−140o= 40o
Z ΔADB α+β= 70o
to w ΔABC 2α+2β= 140o ⇒ γ = 180o−140o= 40o

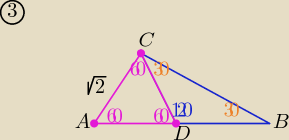 ΔADC jest równoboczny o boku dł √2 ⇒ |DC|= √2
miara kąta BDC= 180o−60o= 120o to:
miara kąta DCB= 30o
zatem ΔDBC jest równoramienny o ramionach |DC|=|DB|= √2
ΔADC jest równoboczny o boku dł √2 ⇒ |DC|= √2
miara kąta BDC= 180o−60o= 120o to:
miara kąta DCB= 30o
zatem ΔDBC jest równoramienny o ramionach |DC|=|DB|= √2
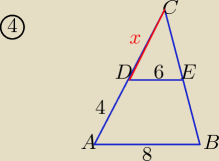
| 8 | 4+x | |||
Z tw. Talesa: | = | ⇒ 8x=24+6x ⇒x= 12 | ||
| 6 | x |


