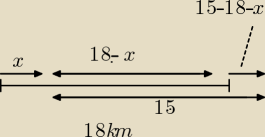
Pomoc Exss: Pojutrze sprawdzian. Mam problem z kilkoma zadaniami. Dla was proste : ). Jacek i Wojtek mieszkają w miejscowościach A i B w odległości 18km. Wyruszając jednocześnie naprzeciw siebie spotykają się po 3 godzinach. Wyruszając jednocześnie w tym samym kierunku po 3 godzinach dzieli ich 15 km. Z jaką idzie prędkością każdy z chłopców. Mam rysunek do tego. Moje pytanie brzmi czy dobrze to zrobiłem. I co dalej. Kolega mi pisze że

18−x		15−18−x
	=		. Dlaczego tak ?.
3		3

Oraz zadanie.

⎧	x−|y−4|=4
⎩	|x−3|+|y−4|	=3

Zrobiłem to graficznie. Z pierwszego wychodzą dwie proste, z drugiego romb. Rozwiązaniem są punkty które są wspólne. Ale jak to zrobić algebraicznie?. Rozwiązując to graficznie mam z pierwszego równania: y=8−x i y=x. Z drugiego y=10−x, y=x−2, y=x+4 i y=−x+4. I nie wiem jak to zrobić bez rysowania.

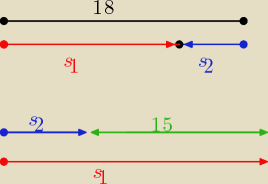
Basia: ad.1 zrobię inną metodą (to jest metoda "na rozum") 3v₁ + 3v₂ = 18 /: 3 3v₁ − 3v₂ = 15 /: 3 v₁+v₂ = 6 v₁−v₂ = 5 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 2v₁ = 11

	11
v1 =		= 5,5
	2

v₂ = 6−5,5 = 0,5 a z równania, które podał Ci kolega jest sprzeczne

Basia: ⎧ x−|y−4|=4 ⎩ |x−3|+|y−4| =3 algebraicznie musimy rozważyć różne przypadki: 1. y−4≥0 i x−3≥0 ⇔ y≥4 i x≥0 wtedy mamy x −(y−4)=4 x−3+y−4 = 3 x−y = 0 x+y = 10 −−−−−−−−−−−−−−−− 2x=10 x=5 y=5 założenia spełnione czyli mamy pierwsze rozwiązanie x=5; y=5 2. y−4<0 i x−3 ≥0 ⇔ y<4 i x≥3 wtedy mamy x−[−(y−4)]=4 x−3+[−(y−4] =3 x+y − 4 = 4 x−3−y+4 = 3 x+y=8 x−y = 2 2x = 10 x=5 y=3 założenia spełnione czyli mamy pierwsze rozwiązanie x=5; y=3 3. y−4≥0 i x−3<0 ⇔ y≥4 i x<3 4. y−4<0 i x−3<0 ⇔ y<4 i x<3 (3) i (4) już sobie sam policzysz powodzenia