zad :): Umie ktos rozwiazac 1 zad? http://www.im.pwr.wroc.pl/~sulkowsk/Lista2pskp.pdf

:): ostatnie d) wiem jak

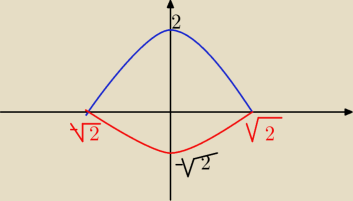
Basia: 2−x²≥0 ⇔ x∊<−√2; √2> i masz _{−√2−x²}∫^2−x2 [ _−√2∫^√2 f(x,y) dx ] dy y = 2−x² ⇒ x²=2−y ⇒ x=±√2−y y=−√2−x² ⇒ y² = 2−x² ⇒ x² = 2−y² ⇒ x=±√2−y² i musisz rozbić na dwie całki _{−√2−y²}∫{√2−y² [ _−√2∫⁰ f(x,y) dy ] dx + _−√2−y∫^√2−y [ ₀∫² f(x,y) dy ] dx pozostałe mogę pomóc Ci rozwiązać mniej więcej za godzinę, ale napisz mi tutaj funkcje bo nie wiem dlaczego ale wiesza mi się przeglądarka na tym pliku pdf

:): Dzieki jestes jeszcze?

Krzysiek: b)http://www.wolframalpha.com/input/?i=%7By%3Dlnx+%2C+y%3D1-x+%2C+x%3D2+%7D a z wykresu to już chyba jesteś wstanie określić granice całkowania?

:): a to pierszamasz dorze napisane w goole?

:): to pierwsze jets dobrze napisane?

:): przy calce f(x,y) to nei oznacza ze cos juest zmienne?

:): √2−x2∫2−x2 [ −√2∫√2 f(x,y) dx ] dy ten zapis ajets ok?

:): to ozancza ze calkujemy po stalym y?

:): Ale wedlug granic tak nie jest

Krzysiek: tak powinno być odwrotnie (to co Basia napisała ) tzn: zamienić granice całkowania w obu całkach i zamienić dx z dy czyli: ∫−√2√2 (∫−√2−x2 2−x2 f(x,y) dy )dx

Basia: czy Ty rozumiesz co to są całki iterowane ? zapis ∫ [ ∫ f(x,y) dx ] dy oznacza, że najpierw całkujesz po x traktując y jak stałą i wtedy granice tej całki "w środku" są stałe a potem całkujesz po y i granice całki zewnętrznej są zmienne zapis ∫ [ ∫ f(x,y) dy ] dx odwrotnie i wtedy stałe są granice całkowania po y a zmienne po x to tak jakbyś sobie obrócił układ z wykresem o 90 stopni a co mają do tego granice ?

:): Krzysiek o to mi chodzilo

:): Tak rozumiem tylko zle napisalas

Krzysiek: no tak Basia, tylko, że masz: ∫[∫f(x,y)dx ]dy i całkujesz po 'x' a potem całkujesz po 'y' i w granicach całkowania masz 'x' to otrzymasz jakąś funkcję h(x) a nie pole (liczbę )

:): dokladnie dzieki krzysiek

:): Krzychu ogarniasz 2.12 i 2.13 co w takim czyms sie robi

Basia: Treść zadania jest taka: Całkę podwójną zamienić na całki iterowane. O polu ani słowa

:): Ale zle napisalas po prostu

:): wedlug zapisu pierwszego y potraktowalas jako stale a x zmienny a tak na prawde granice dalas zle

:): dobra mniejsza o to zle jets i tyle

Basia: a faktycznie; zamieniłam dx z dy; trzeba poprzestawiać

:): uf

:): to pomozcie z tymi 2.12 i 2.13 jakiego typu to rownania?

Krzysiek: 2.12 zwykłe równania liniowe jednorodne 2.13 niejednorodne aby rozwiązać równanie niejednorodne, rozwiązujesz jednorodne a potem metoda uzmienniania stałej lub metoda przewidywań 2.13 a)y'' +3y' −10y =te^2t równ jednorodne: y'' +3y' −10y =0 równ. charakterystyczne: r² +3r−10=0 Δ=49, r₁ =−5 r₂ =2 czyli: y₁=e^{r₁ t} =e^−5t y₂ =e^{r₂ t} =e^2t zatem rozw. równ jednorodnego to y=c₁ y₁ +c₂ y₂ rozw. niejednorodnego szukasz w postaci: y=t(at+b)e^2t

:): Mozna jeszcze jakis przyklad 2.12?

Krzysiek: wystarczy rozwiązać równanie charakterystyczne jak Δ>0 to y₁ =e^{r₁ t} y₂ =e^{r₂ t} Δ=0 to y₁ =e^{r t} y₂ =te^{r t} Δ<0 r=α+/− βi y₁ =e^αt cos(βt) y₂ =e^αt sin(βt)

:): o ludziexd cot ot jest

Krzysiek: wzory które musisz umieć,na pewno musiałeś mieć je na wykładzie/ćwiczeniach (być może nawet uogólnione na równanie n−tego rzędu )

:): ho ho ho dobra dizkei

:): Moze ktos zrobic reszte przykaldow albo sprawdizc czy ja robie ok?

Krzysiek: możesz napisać swoje rozwiązania to ktoś sprawdzi lub wpisać równania np. do http://www.wolframalpha.com/ to otrzymasz wynik

:): Czyli przy jednorodnych czyli tam gdzie jest 0 po prawej rozwiazujemy rownanie kwadratowe liczymy pierwisatki i potem rozpatrujemy dla delty wiekszej mniejszej i rownej 0? czy juz nie

:): b) 2.12 r²+r=0 r=0 i r=−1?

:): co dalej w roznnaiach jednorodnych?

:): Moze ktos zrobic 1 przyklad?

Krzysiek: 2.12 b) równ charakterystyczne to r² +3r =0 r(r+3)=0 więc r₁ =0 , r₂ =−3 więc y₁ =... y₂ =...

:): no wlasnie y= co?

Krzysiek: a co wyżej napisałem? jak mamy dwa rozwiązania to...

:): a i w zad 2.2 w punkcieb mozesz napisac tylko calke mi wyszlo 3 y−2 ∫dy∫e^xdx 2 y

:): zatem rozw. równ jednorodnego to y=c1 y1 +c2 y2

:): jak Δ>0 to y1 =er1 t y2 =er2 t

:): czyli y₁=e⁰ y₂=e^−3t

Krzysiek: równ. różniczkowe ok, ale całka nie, powinny wyjść 3 całki (przedział dla 'y' rozbić na 3 przedziały )

:): powaznie?

:): ok spoko

Krzysiek: co do równ. różniczkowego to jeszcze stałe: c₁ ,c₂ musisz wyliczyć wstawiając warunki początkowe do rozwiązania równ. jednorodnego

:): 2.3 przyklad c

:): czyli?

:): podzielilam obszar na 2 robie po stałym y zmiennym x ierwszy przedzial 1 2 ∫ dy ∫ f(x.y)dx 1/2 1/y

:): 2 y +∫dy∫dx 1 2

Krzysiek: y(0)=0 0=c₁ y₁ (0) +c₂ y₂ (0) y'(0)=6 więc obliczasz pochodną za t wstawiasz 0 i przyrównujesz do 6 2.3 c)druga całka po dx to granice odwrotnie (poza tym, jakbyś całkował po 'dx' to miałbyś tylko jedną całkę )

:): c1+c2=6?

Krzysiek: to jest pierwsze równanie jeszcze drugie potrzebujesz

:): dobra to nei dla mnei nei ogarne tego