planimetria Aga: W trójkącie prostokątnym ABC, w którym kąt C=90 stopni i |BC|<|AC| poprowadzono prostą przez wierzchołek C trójkąta, która przecina przeciwprostokątną w punkcie D takim, że |AD|: |DB|=2:1. Oblicz długość przeciwprostokątnej, jeśli |BC|=√3 cm i |kąt DCB|=30 stopni

Eta: Pomagam, rysuję

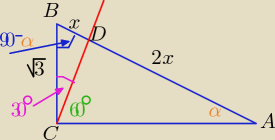
Eta: |AB|= 3x , x>0

	x		|CD|		|CD|
ze wzoru sinusów (*)		=		=
	sin30o		sin(90o−α)		cosα

	2x		ICD|
oraz: (**)		=
	sin60o		sinα

	2sinα
(*) |CD|=2x*cosα i (**) |CD|=
	√3

to porównując równości otrzymasz:

	2sinα
cosα=
	√3

z jedynki trygonometrycznej: sin²α+cos²α=1

	4sin2α
sin2α+		=1 /*3
	3

	3
3sin2α+4sin2α=3 ⇒ sin2α=
	7

	√3
to przyjmujemy: sinα=		bo α € (0,90o)
	√7

	√3		√3
sinα=		=		⇒ |AB| = √7
	|AB|		√7

Aga: dziękuję

Eta:

	4xsinα
Poprawiam w (**) ma być: |CD|=
	√3